2021. 1. 6. 16:54ㆍ딥러닝 강의 정리
RNN의 강점

위에서 행이 output, 열이 input이라고 해보자. 그리고 각각의 색칠된 곳의 의미는 2진법 계산에서 예를들어 0+1=01임으로 input이 01, output이 01인곳에 색칠이 되있는 것이다. 위와 같은 이진법 계산을 MLP를 이용해 training을 해본다고 생각하면 우리는 1비트짜리 2개의 input계산을 위해서 2^4만큼의 training data가 필요할 것이다. 모든 패턴을 보아야 하기 때문이다. 만약 2비트짜리 2개 계산이라면 여기서 필요한 training data는 exponential하게 증가할 것이다. 또한 MLP자체가 고정되어있음으로 위의 경우에서 만약 2비트짜리 input 2개를 넣으면 에러가 날 것이다.
그렇다면 이러한 경우를 RNN을 이용하여 훈련시키면 어떻게 될까?

MLP에서는 N개의 비트를 input으로 받는다할때 N+1개의 output을 한꺼번에 낸다. 하지만 RNN은 시간에 따라 나옴으로 한비트씩 결과가 나올 것이다. 따라서 input의 비트수가 달라져도 상관이 없다. RNN을 그만큼 더 돌리면 되기 떄문이다. 또한 필요한 training data수 역시 2개 input짜리 RNN unit을 만들어서 훈련시킨 뒤에 그것을 계속 사용하면 된다. 그래서 필요한 traninig data수역시 굉장히 줄어들게 된다.
XOR문제를 보면

아래의 수많은 input을 한꺼번에 받은뒤에 output을 계산한다. 하지만 XOR의 네트워크는 아래와 같이

4개의 input만 해도 9개의 뉴런이 필요한데 위와같이 10개의 input은 더 복잡한 네트워크를 구성할 것이다. 또한 이역시 input의 사이즈가 고정되어 11개의 input이 들어온다면 결과도출을 하지 못할 것이다.
하지만 RNN에서는

input bit를 한꺼번에가 아닌 차례대로 받아서 전의 bit와 비교하여 구할 수 있다. 따라서 위의 모양의 RNN unit하나만 완성하면 input bit가 수천개라도 위의 RNN unit을 수천개를 recurrence하게 배치하여 구할 수 있다. 이때 trainig data는 위의 RNN unit 즉 2개의 input일때만 training 시키면 된다.
BIBO Stability

위의 네트워크는 time-delayed network이다. 이 네트워크는 input이 bounded 하다면 output 역시 bounded 할 것이다. 이때 Bounded Input Bounded Output의 성질을 BIBO Stability라고 한다. BIBO stability일때는 input이 explode만 하지 않는다면 output 역시 explode 하지 않을 것이다. 따라서 매우 좋은 성질이라고 할 수 있다.
그렇다면 RNN은 BIBO일까?

Time delayed와 달리 RNN은 모든 시간대의 정보를 가지고 있다. 따라서 output과 hidden activation이 bounded라면 어느 순간 수렴을 해버릴 것이다. RNN이 linear system이라고 생각해보자. 이때 모든 activation은 identify function이다.

k번째의 hk는 아래와 같이 형성될 것이다.


이 나온다. 위의 과정을 h_-1일때까지 반복하면

가 나오게 된다. 이때 를 보면 initial condition인 h_-1이 0이고 나머지 input x_1, x_2...가 0일때의 RNN에 넣었을때의 결과이다.
을 initial condition과 자기이외의 input이 0일때 RNN network에 넣었을때의 결과라고 하면 아래의 식으로 바뀌게 된다.

그리고 이 네트워크가 linear하다고 가정하였음으로 안에 있는 식이 밖으로 나올 수 있다. 그래서 아래로 바뀌게 된다.
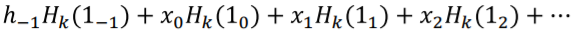
다시한번정리하면 는 k시간에 input이 [000...10.00] (1은 t번째에 있다)이고 initial condition이 0일때 의 hidden response이고 위와같은 superposition 형태로 나타낼 수 있는 것이다. 여기서 h_-1은 initial condition을 t=-1로 보고 구한 것이다. 결국 위의 식의 의미는 k시간의 hidden layer의 output은 t라는 시간 이외의 input은 다 0으로 두고 구한다음 그것을 다 더한 것과 같은 것이다. 따라서 t=0일때만 생각하고 구하고, t=1일떄만 생각하고 구하고 이런식의 superposition의 형태로 나타낼 수 있는 것이다. 이덕분에 BIBO를 알아보고자 할때 t=0일때 이외의 input은 다 0으로 두고 구해보아도 나머지도 이때의 성질을 따를 것이기 때문에 간단하게 구할 수 있게 된다.
이를 그림으로 표현하면 아래와 같이 나타낼 수 있다.

위에처럼 표현되면 t=0일때만 single input을 준다면 의 식이 만들어지고 우리는
만 살펴보면 되는 것이다. 이때 blow up하면 전체 시스템이 blow up하는 시스템인 것이다.
h(t)가 simple, scalar, linear recursion인 이라면 k=0일때만 input이 들어올때 t 시간의 hidden layer의 output은

이런 구조를 통해 가 나오게 된다. 이를 그래프를 그려보면
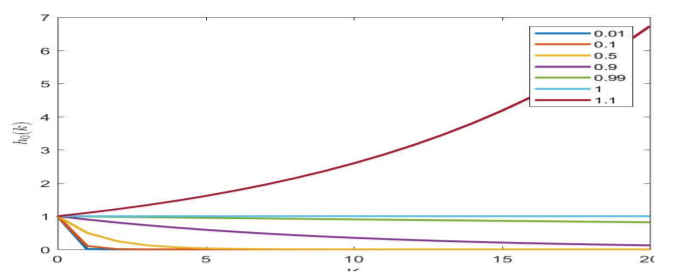
w>1일때는 blow up이고 w=1일때는 일정, w<1이면 0으로 수렴하는 모습을 볼 수 있다.
이것을 벡터의 관점에서 보면 어떠할까? 우선 Vector linear recursion은 아래와 같다.

위에서의 표현과 다를 것이 없다. linear recursion은 W에 어떠한 값이 곱해지면 방향은 일정해야 한다. 여야 하고 이는 eigen decomposition인
로 구할 수 있다. Cx를 x'이라고 두면
에서 ui부분이 x'자리임으로 x'를 eigen vector로 나타낼 수 있다.


이고 이를 계속 반복하면

가 나오게 된다. 여기서 t를 무한대로 보내버리면 의 항에서 람다값이 가장 큰 부분이 가장 커지고 나머지는 그것에 비하면 값이 굉장히 작아짐으로 0이라 생각할 수 있다. 따라서

의 식을 얻을 수 있다. 위에 의하면 blow up할지 안할지는 W의 eigen value중 가장 큰 값이 결정한다는 것을 알 수 있다. 만일 그 값이 1보다 크다면 blow up이고 작으면 0으로 수렴하는 것이다.
그렇다면 activation이 non-linearity를 가지고 있다면 어떻게 될까? sigmoid로 예를 들어보면 우선 h에 대한 식은 로 적을 수 있다. 초기값을 아래와 같이 잡고

이를 계속 반복하면

어느 한점으로 수렴을 한텐데 그점은 가중치인 W에 dependent할 것이다. 이러한 방식으로 Tanh와 Relu모두 같은 조건에서 실험을 해보면 아래의 결과가 나온다.

Sigmoid는 굉장히 빠르게 converge하고 Tanh는 그에비해 속도가 느렸으며 Relu는 blow up하는 경우도 있었다. 위는 positive부분에서 시작한 것이고 negative영역에서 시작하면 아래의 결과가 나온다.

마찬가지로 Sigmoid는 굉장히 빠르게 converge하고 Tahnh는 그에 비해 속도가 느리고 Relu는 negative영역에서는 0이기때문에 response가 없게 된다.
vector process일때도 마찬가지인데 uniform unit vector()로 시작을 하게 되면


의 결과를 얻게 된다.
위의 결론은 빠르게 converge할수록 기억을 빠르게 잃어버린다는 것인데 이 경우 tanh를 activation으로 사용하는 경우가 가장 좋은 모습을 보였다(하지만 이역시 그리 긴시간을 기억하고 있지는 못하였다). ReLU의 경우에는 blow up의 경우도 있고 아예 response가 없는 경우도 있어서 사용하면 안된다.
h(t) = 0.5h(t-1)+0.25h(t-5)+x(t)같은 deeper recursion의 경우도 좀더 복잡한 수학적 방법을 사용하면 같은 결과를 얻을 수 있다.
Vanishing Gradient Problem
RNN의 gradient vanishing을 보기전 일반적은 depp network를 살펴보자.

다음과 같은 네트워크가 있다고 할때 output vector Y는 다음과 같을 것이다.

그렇다면 divergence는 여기에 divergence function만 붙이면 된다.

이를 미분하기 전 f(Wg(x)를 X에 대하여 미분해보자. 이러한 chain rule을 사용할 수 있고 이것을 간단히 나타내면 Z=Wg(X)라고 하면
로 나타낼 수 있다. 여기서
는 jacobian matix이다.
위를 이용해 Div(x)를 에 대해 미분을 해보면 아래의 식을 얻을 수 있다.

우선 jacobian에 대한 것을 먼저 파악해보자. jacobian matrix는 아래와 같이

모든 component에 대해 편미분을 한 것을 matrix로 나타낸 것이다. 아래와 같이 RNN을 구성할때

hidden layer의 jacobian은 빨간색 matrix가 된다. i=j이외는 모두 0인데 그 이유는 예를들어 (1,2)에서는 를 구해야 되는데 f1은 1번째 layer이고 z2는 2번째 layer이며 f1의 함수의 input은 오직 z1만 있음으로 편미분 한 결과는 0이 된다. 위에서 알 수 있는 사실은 activation function인 f의 derivative(f')가 bounded라면 그의 derivative(여기서 Jacobian)은 항상 bounded될 것이라는 것이다. 우리가 실제로 사용하는 activation인 sigmoid, tanh, ReLU는 모두 1을 넘지 않음으로 bounded이다. 또한 1보다 작음으로 Jacobian은 항상 줄어들을 것이다.
그렇다면 이제 전체적인 네트워크를 살펴보자.

동그라미 친부분이 Jacobian이고 이는 항상 줄어들음으로 backpropagation에서 Jacobian을 거칠때마다 그 값은 계속 줄어들게 될 것이다.
그렇다면
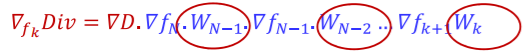
위의 식에서 weight는 어떤 영향을 끼칠까? weight가 1보다 크면 expand될 것이고 작으면 shrink하게 될것이다. 그러므로 backpropagation에서 W를 만날때마다 값은 늘어나거나 줄어들거나 할것이다. 하지만 gradient descent로 W는 backpropagation에서 나온 gradient의 반대방향으로 줄어들 것임으로 계속 진행하면 왠만한 w들은 1보다 작아져 결과가 줄어들 것이다.
위의 결과로 볼때 deep network에서 lower 또는 earlier layer는 아무래도 shrink의 성격을 지닌 jacobian과 weight를 많이 거치다보니 미분 값이 사라지게 될것이다. 그리고 이것은 불안정하게 gradient descent가 되는 결과를 초래할 것이다.

위의 그림은 MNIST를 ELU activation을 이용하여 계산한 것인데 Input layer에 다가갈 수록 값이 사라지는 것을 볼 수 있다.
What About RNN?
RNN은 매우 deep한 네트워크이다. 과거의 모든 정보를 다 가져오기 때문이다. 따라서 위에 처럼 결국은 t=0에서의 미분값은 사라지게 될 것이다. RNN은 또한 forward에서도 위에서 보았다싶이 vanishing 문제가 일어난다.

이렇게 되면 문제가 예를들어 "Jane had a quick lunch in the bistro. Then she..."라는 문장은 RNN에 넣었는데 두번째 문장을 읽어들일때 Jane이 사라져서 she가 누구인지 모르게 되는 경우가 생기게 된다. 따라서 기억하는 시간을 늘려야 되며 필요할때 다시 불러들이는 기능이 있어야 된다.
위의 deep network에서의 vanishing문제를 볼때 weight가 들어가게 되면 아무래도 unstable해진다는 것을 배웠다. 따라서 weight없이 오로지 스위치로만 구동되는 것을 만들려고 한다. 이 스위치는 useful한 메모리를 얼마나 기억할지, 잊을지 등을 결정하게 되는 요소이다.

위의 식처럼 weight가 없고 jacobian도 없어 vanishing문제에 걸림돌을 없에버렸다. 오직 σ의 gating term만 존재할 뿐이다. 이 gating term은 scaling만 할 수 있다. 그리고 이러한 구조를 The Constant Error Carousel이라고 한다.
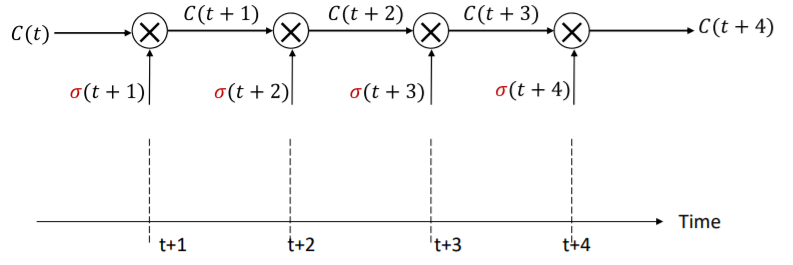
기본적인 구조는 위와 같다. 하지만 이것만으로는 학습을 할수 없음으로 실질적인 non-linear work는 h(t)를 떼어내어 그것을 통해 진행한다.

그리고 gate σ의 input으로 현재의 input, 현재의 hidden state 그리고 다른 stuff들을 받게 된다.

Long Short-Term Memory(LSTM)
그렇게 위를 토대로 LSTM이라는 것이 만들어졌다. 우선 기본적인 RNN의 구조는 아래와 같다.

그리고 LSTM은 아래와 같다.

여기서 σ는 그 메모리가 중요한지 안중요한지를 결정하게 된다. 이제 하나하나 이것을 뜯어서 보자. 이 LSTM에서 가장 중요한 부분은

빨간 박스의 remembered cell state이다. 한부분만 자세히 보면

이렇게 생겼는데 여기서 Ct는 위에서의 constant-error carousel 줄여서 CEC라고 한다. 이것은 non-linear function등에 영향을 받는 것이 아닌 오직 gate의 영향만 받는다. 그렇다면 gate는 무엇일까?

gate는 이렇게 생겼으며 시그모이드의 output이 0-1임으로 그 결과값을 곱해주기만 하는 것이다. 이 값에 따라 정보가 중요한지 안중요한지가 결정이 된다.
이제 하나씩 보면

위는 Forget Gate이며 과거의 정보를 계속 들고 갈지 잊어버릴지를 결정한다. 좀더 정확히는 얼마나 과거를 가져갈까를 결정한다.

위는 Unput Gate이며 기억할 가치가 있는지를 결정한다.

그리고 위의 과정을 거쳐 Memory cell을 update한다. 여기서 두번째 input이 두부분으로 나누어져 있는데 input에 특ㄱ별한게 있는지 결정하고 기억할 가치가 있다고 판단되면 memory cell에 더하는 구조이다.

이것은 Ouput과 Output Gate이며 output을 tanh를 이용하여 -1과 1사이로 만든다. 그리고 output gate로 메모리 cell에 들어있는게 지금 출력될만한지를 결정한다.

또한 C를 그대로 가지고 와서 진행하는 경우도 있다. 이것을 Peephole Connection이라고 한다. 그래서 전체적인 모습은 아래와 같다.

위의 구조를 조금 간단히 만들 수 있는데

이렇게 forget과 input gate를 합치고

output gate를 thanh로 압축하지 말고 그냥 C값에서 빼오는 방법으로

이렇게 좀더 간단한 구조로 만들 수 있다. 이를 Gated Recurrent Units, GRU라고 한다.
'딥러닝 강의 정리' 카테고리의 다른 글
| Sequence to Sequence Models/Lec.12 (0) | 2021.01.07 |
|---|---|
| Recurrent Networks Part3/Lec.11 (0) | 2021.01.07 |
| Recurrent Networks 1/Lec. 10 (0) | 2021.01.06 |
| Convolutional Networks 3/ Lec.09 (0) | 2021.01.05 |
| Convolutional Networks 2/ Lec.8 (0) | 2021.01.05 |