2021. 1. 6. 01:05ㆍ딥러닝 강의 정리
Speech recognition, document analyze, identify topic, 주식 시장 예측등은 앞에서의 CNN으로는 한계가 있다. 앞에 언급한 것들은 모두 시간의 순서라는 조건이 붙기 때문이다. 이들을 네트워크에 넣는다면 input은 sequence of vector이 될 것이다.
주식 시장 예측 네트워크를 예를 들어보자. 주식 시장을 예측하려면 현재도 중요하지만 과거의 패턴 또한 중요하다. 따라서 아래처럼 나타낼 수 있다.



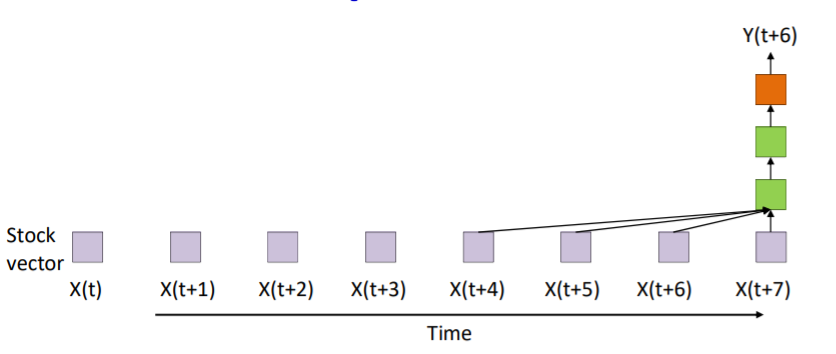
위는 과거 3개분의 시간과 현재를 input으로 넣은 convolution neural network이다. 위와 같은 모양을 CNN때 보았는데 Time-Delay nerual network이다. 여러개의 input을 동일한 네트워크에 넣으면서 scan 하는 것이다. 또한 들어가는 input의 갯수가 유한하기 때문에 finite response system이라고도 한다. 위의 식은 아래와 같다.

위의 네트워크는 하나의 문제가 있다.

input의 갯수가 유한하기 때문에 빨간색 박스의 날이 네트워크에 들어가지 않는다. 이날 중요한 패턴이 있을 수 있는데 학습하지 못하는 것이다. 그래서 과거 모든 날을 input으로 넣자니 불가능하였다.

NARX Network
그래서 과거를 기억하는 memory역할을 만들자는 취지에 아래의 NARX Network가 나왔다. 이 네트워크의 식은 아래와 같다.

Yt의 output은 과거의 모든 Y와 X가 모여서 만들어지는 것이다.

우선 X0의 input으로 Y0가 생성된뒤

그다음 input과 Y0가 만나 새로운 Y1을 생성한다. 그리고 이 과정을 계속 반복하는 것이다. 그리고 그 결과는 아래와 같다.

그래서 일반적으로는 몇개의 과거만 input으로 놓는 방식을 사용한다.

이러한 네트워크는 날씨, 주식시장등에서 많이 사용된다. 하지만 이 네트워크의 단점은 네트워크의 output이 과거의 정보이지 네트워크 안에는 그러한 정보를 담든 부분이 없다는 것이다.
Other Networks : Jordan, Elman
그래서 이를 보완하고자 memory variable이 나왔다. 이것은 오직 과거를 기억하는데 사용하는 요소이다.

여기서 mt가 memory variable인데 과거의 정보를(t-1) 특정 함수를 통해 저장하는 것이다. 이를 이용해 Jordan Network가 나왔다.

여기서 파란 cell의 역할은 단지 과거의 running average를 기억하는 것이다. 하지만 기억이외의 아무런 역할이 없고 learnable하지 않아 backpropagation때는 아무런 반응이 없다.
그리고 Elman Network도 나왔다.

Jordan과 달리 memory 부분이 output과 분리가 되었다. 또한 learnable하긴 한데 초록색 cell과 파란색 cell은 clone이여서 완벽히 같은 cell이다. 따라서 이부분은 학습이 안되고 파란색 cell이 다음 layer의 초록색 cell과 연결되는 부분만이 학습이 가능하다.

또한 이렇게 slice단위로 끊기는데 각 slice가 유기적인 연결이 없고 independent하다는 단점이 있다.
The State-Space Model : RNN
위에서의 모델들을 바탕으로 무한개의 과거를 다루는 infinite response systme이 생겨났다. 이것을 state-space model이라고 한다. 우선 아래의 식을 보면

h_t는 네트워크의 state를 나타낸다. 당연히 h_-1의 initial state를 먼저 정의를 해야한다. 이 state는 전체 과거의 정보를 요약하는 기능한다. 이것을 (fully) recurrent neural network라고 하고 줄여서 RNN이라고 한다. 구현 방법은 굉장히 다양한데 아래 네트워크가 가장 기본적인 것이다.

초록색 cell이 state인데 이것은 과거 직전 시간의 state와 현재의 input을 받아서 형성된다. 따라서 이 구조로 볼때 t=0일때의 input이 계속 모든 output에 영향을 끼칠 수 있는 것이다. 초록색 state cell은 이렇게 한개로 구성되는게 아니라 여러개 그리고 바로직전의 state가 아니라 여러 시간전의 state를 다 받을 수 있다. 아래는 응용한 것들의 예이다.

위는 2개의 hidden layer로 state를 가졌다.



위의 구조는 NARX랑 비슷하게 생겼다.
사실 위의 구조들은 time에 따라서 펼쳐 놓은 것이고 하나의 모델로도 표현이 가능하다.

이렇게 빨간색이 recurrence를 의미해 다음 layer에 영향을 주는 것이고 검은색선은 현재 시간에서 이동되는 것을 나타낸다.


위와 같은 식으로 하나의 모델로도 나타낼 수 있다.
그렇다면 계산하는 방식은 어떻게 될까? 가장 간단한 모델부터 살펴보자.

는 (1)번째 hidden layer를 나타낸다. recurrence됨으로 X로 부터 받은 input의 weighted sum과 바로 전 t-1일때의 h의 weighted sum의 합으로 이루어진다.
2개의 hidden layer로 이루어진 네트워크도 마찬가지이다.

여기서 의 의미는 바로전의 2번째 layer에서 현재의 2번째 layer로 넘어왔다는 것을 의미한다.

이런 복잡해보이는 형태도 원리는 같다.
Variants on Recurrnet Nets
RNN는 여러가지 구조로 나타낼 수 있다. 대표적인 것들 몇개를 살펴보면

하나의 input과 하나의 output으로 구성된 Conventional MLP

하나의 input과 여러개의 output으로 이루어진 Sequence generation, 이것은 image에 caption을 붙일때 주로 사용된다.

여러개의 input과 하나의 output으로 이루어진 Sequence based prediction or classification, 이것은 음성 인식이나 텍스트 분류에 주로 사용된다.

이것은 delayed sequence to sequence라고 하며 machine translation에 주로 사용된다.
또한 같은 many to many이지만 delay가 없는

Sequence to sequence는 위에서 본 주식 문제등에 주로 사용된다.
Train the RNN
RNN은 시간을 기반으로하기 때문에 학습도 Back Propagation Through Time(BPTT)를 이용해 한다. 우선 forward path는 아래와 같다.

또한 그에 대한 코드는 아래와 같다. 여기서 Wc는 current time의 weight이고 Wr은 previous time에 사용하는 recurrent weight이다.

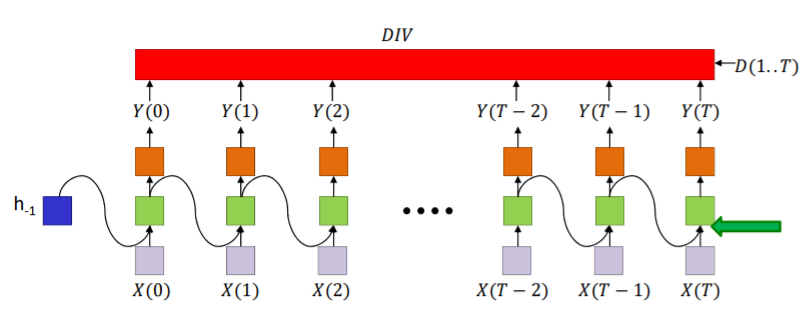
이제 BPTT를 해보자. 우선 Divergence 값을 구해야 한다. 이때의 divergence값은 각각의 시간별로의 divergence들의 합이 아닌 전체 결과를 통째로 이용해 구해야 한다.

우선 네트워크는 one hidden layer로 정하였고 Y(t)는 output, Z(2)는 t시간에서 output layer로 들어간 값
제일 첫번째 단계는 를 구하는 것이다. 하지만 DIV는 모든 0~t시간까지를 이용한 값이고 Y(T)는 한 부분의 시간만을 이용하는 것임으로 구하기가 쉽지 않다. 그래서 아래처럼 divergence를 각가의 시간의 divergence에 대한 합으로 가정하고 진행한다.

위에처럼 만듬으로 가 되었다. 이렇게 첫번째 step인 DIV를 우리가 계산한 결과Y로 미분한 값을 구했다면 그다음은 DIV를 hidden layer의 output값으로 미분한 것을 구할 차례이다.(위의 화살표). 이것은 chiain rule에 의해 아래의 식으로 구할 수 있다.

여기서 sum이 되어있는 이유는 벡터 미분의 정의를 생각해보면 된다.

위에 처럼 모든 요소들을 미분한 다음 더해주기 때문이다. 그 다음단계는 hidden layer의 output인 h(t)에 대해 미분하는 과정이다.

Z(2)는 hidden layer의 결과인 h(t)를 weighted sum한 결과이다. 따라서 거꾸로 가보면 아래와 같을 것이다.

위에서 이번에는 DIV를 w(2)에 대해서 미분을 할 수도 있다. 이떄는 반대로 w대신 h가 곱해질 것이다.

이번에는

위의 초록색부분을 살펴보자.
위에서 hi에 대하여 미분한 결과를 이용하여

로 나타낼 수 있다. 그다음으로 가보자. 그 아래부분은 input이 2개 이다. 그래서 2개의 경우를 각각 계산해주어야 한다.

이렇게 input이 X일때는 간단히 아래처럼 나타낼 수 있다. 이므로
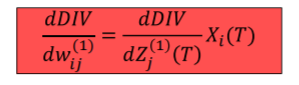
로 나타낼 수 있다.

이렇게 input이 recurrence 부분일 때는 마찬가지로

이다. 이제 T-1일때로 가보면


위의 두 부분은 위에서 제시한 방법과 같은 방법으로 풀 수 있다.

위와 같은 weight부분은 조금 다르다. 위의 화살표 위치인 w(2)는 위에서 이미 구했다. 따라서 그 이후에 구해지는 w(2)는 앞의 layer에서 구한 값에 더해주기만 하면 된다.

그 아래의 계산은 다음과 같다.


이때도 역시 앞에 layer에서 w(1)을 구했으니 그 결과에 더해주면 된다.

위의 과정을 h-1까지 반복하면 된다.

위의 과정을 종합해보면 아래의 식으로 정리할 수 있다.

Bidirectional RNN
위에서의 RNN이 한방향으로 움직였다면 Bidirectional RNN은 양방향으로 움직인다. 즉 내가 t라는 시간에 있다면 t+1에 에 있는 일을 t시간의 형태로 바꿔서 계산을 하는 것이다. 그 과정은 아래와 같다.

이를 계산하는 법은 두개를 따로따로 구한다음 마지막 output을 구할 때 합치면 된다. 그 코드는 아래와 같다.

Backpropagation과정은 다음과 같다.
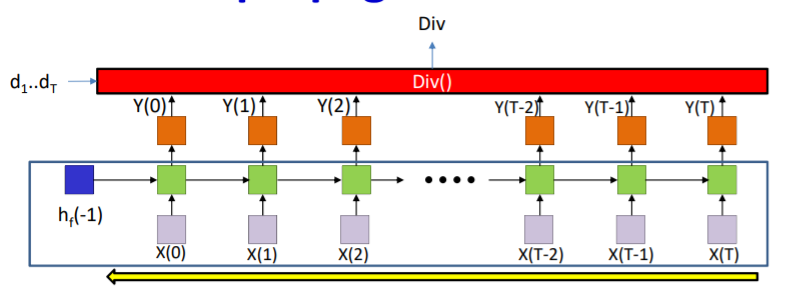
forward 뱡향으로 backpropagtaion 하고

backward 방향으로 backpropagation을 해주면 된다. 그리고 그 나온 값들을 계속 더해주면 된다. 그에 대한 코드는 다음과 같다.


forward net에 대한 BPTT 함수를 만든뒤 backward net은 시간만 거꾸로 해서 넣으면 된다.
'딥러닝 강의 정리' 카테고리의 다른 글
| Recurrent Networks Part3/Lec.11 (0) | 2021.01.07 |
|---|---|
| Recurrent Networks: Stability analysis and LSTMs/ Lec.11 (0) | 2021.01.06 |
| Convolutional Networks 3/ Lec.09 (0) | 2021.01.05 |
| Convolutional Networks 2/ Lec.8 (0) | 2021.01.05 |
| Training Optimizers and Regularizers/Lec 7. (0) | 2021.01.03 |