Training Optimizers and Regularizers/Lec 7.

Momentum and Incremental updates

앞에서 incresmental update는 각각의 샘플을 따로 다루기 때문에 variance가 크다고 하였다. 그리고 모멘텀을 생각해보면 running average of gradient를 이용하기 때문에 oscillation이 부드러워지고 덕분에 variance가 줄어드는 효과가 생긴다. 그렇다면 이 두개를 섞으면 더 좋은 효과가 나지 않을까? 그 코드가 아래의 코드 이다.

랜덤하게 샘플들을 두고 미니배치를 만든다음 각 미니배치별로 loss값을 구한다. 그리고 모멘텀을 구하기 위해 average를 구한뒤 업데이트를 하면 된다. 

앞에서 모멘텀을 좀더 효율적으로 구현하는 법이 Nestorov Accelerated Gradient라고 하였다. 이 방법은 모멘텀 방법의 순서를 살짝 바꾼 것인데 이 역시 incremental update와 함께 사용하면 매우 효율 적이다. 

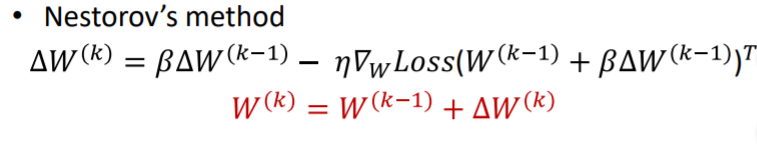
Higher Order Methods

앞의 momentum과 nestorov는 모두 average 즉 1st momentum을 이용한 방법이다. 최근에는 2nd momentum(variance)를 이용한 방법도 많이 개발되었다. 

위의 경우에서 변동성이 큰 y축방향의 step을 줄이고 변동성이 작은 x축의 step을 늘리는 방법이다. 그리고 그 변동성은 variance에 기반을 한다. 여기서 나온것이 RMS Prop이다. 우선 약속을 하나 하는데 앞으로 사용할 squared derivative를 아래의 식으로 사용하는 것이다. 

2nd derivative가 아니다. 그리고 mean squared derivative는 아래와 같다. 

RMS Prop은 mean squared value of derivative를 계속 계산하면서 가지고 있는다. 그리고 그 계산을 이용해 learning rate를 normalize해 업데이트를 진행한다. 

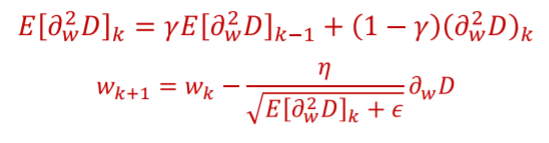
이 방법을 계속 진행하면 변동성이 점점 줄어듬으로 언젠가는 방향만 남게 될 것이다. 그렇다면 그때는 RProp과 같아지게 된다. RMS Prop의 코드는 아래와 같다.

위의 방법은 그러나 2nd momentum만 사용한 것이다. 그렇다면 1st와 2nd moment를 둘다 사용하는 방법은 없을까? 그것이 ADAM이다. ADAM은 momentum method와 RMS Prop을 섞은 것이라고 볼 수 있다. 아래 업데이트 방향을 보면 더 쉽게 이해 할 수 있다. 

m은 mometum의 방법을 가져왔고 v는 RMS Prop의 방법을 가져와 그 두개를 이용해 업데이트를 진행한다. 여기서 는 큰 의미가 있는 것이 아니라 값이 사라지는 것을 방지하기 위해 나누어 준 것이다. 

 

To Make Network Converge Better

Network가 Converge를 더 잘 할 수 있게 하는 것은 몇가지 방법이 있다. 

 

1. Divergence Function

우선 Loss function의 식을 다시 살펴 보자.

divergence function의 평균이 Loss function이다. 따라서 convergence는 곧 divergence function에 달려있는 셈이다. 그렇다면 converge하기 좋은 함수는 어떤 것일까?

왼쪽처럼 많은 local optima가 존재하면 안되고 optimum에 멀리에 low slope가 있어도 안된다. 이 경우 converge하려면 optimum에 가야하는데 low slope에 걸려서 시간이 오래 걸릴 것이다. 또한 optimum 근처에 high slope가 있어도 안된다. gradient descent는 learning rate가 loss값이 비슷하면 점점 줄어들기 떄문에 아래 그림처럼 converge하는데 시간이 오래 걸리고 overshooting의 가능성도 생긴다. 

따라서 아래 그림처럼 smooth하게 convex한 function이 가장 좋다. 

이러한 성질은 divergence functino으로 어느정도 만들 수 있다. 지금까지 배운 divergence functino은 두가지가 있는데 하나는 L2이고 나머지 하나는 KL이다. L2는 regression에 이용되고 KL은 classification에 이용된다. 

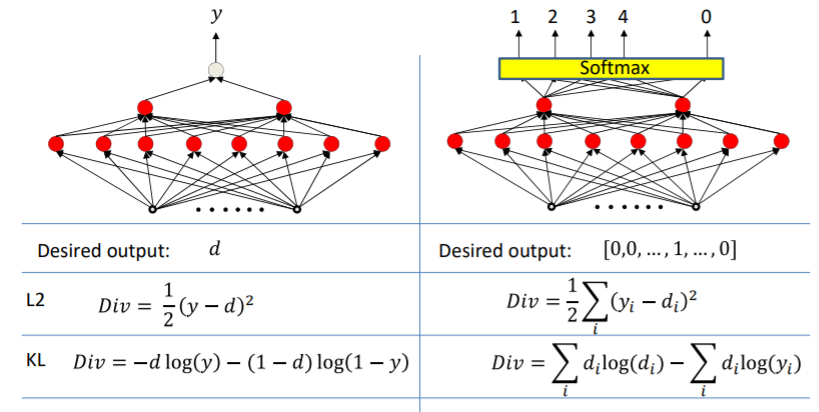
그리고 clssifier을 L2와 KL을 사용하였을때 single perceptron의 plot은 아래와 같다. 

L2는 완벽한 bowl 형태는 아니고 KL은 convex하다. 따라서 이떄는 KL을 사용하는 것이다. 상황에 맞게 적절한 divergence function을 사용해야 converge가 더 잘 된다. 

 

Batch Normalization

Training할때 training data가 모두 같은 분포를 가지고 있다고 가정한다(예를 들어 Minibatch). 하지만 실제로는 모든 minibatch들은 서로 다른 분포를 가지고 있고 그래서 이전 layer의 변화로 인해 현재 lyaer의 입력 분포가 바뀌는 현상이 생길 수 있다. 이것을 Covariate shift라고 한다. 그리고 이것은 training에 매우 나쁜 영향을 끼친다. 이를 막기 위하여 모든 batch들을 평균이 0이고 표준편차가 1로 옮긴다.  그다음 그 것을 적절한 위치로 shift 시킨다. 이것이 Batch Normalization이다. 

이러한 Batch Normalization 기법은 weighted sum과 activation function 사이에 사용된다. 그리고 그것에 대한 그래프는 아래와 같다. 

weighted sum의 결과에 평균을 뺴고 분산을 나누어서 normalize를 한뒤에 r만큼 scaling하고 베타값만큼 shift를 하는 것이다. 평균과 표준편차는 아래와 같이 구할 수 있다. 각각의 미니배치 크기 만큼 구하면 된다. 

그렇다면 이것의 derivative는 어떻게 될까? 우선 일반적인 minibatch때의 derivative를 보면 아래와 같다.

하지만 위에서 Batch Normalization을 사용하면 좀더 복잡해지는데 새로 계산된 결과에는 평균과 표준편차가 반영이 되있기 때문이다.

이제 Back propagation을 위해 그래프를 한번 살펴보자.

위와 같이 복잡하게 얽혀있다. 위를 좀더 간략하게 나타내면 아래와 같다.

먼저 weighted sum까지의 backpropagation을 보면 아래와 같다. 

그다음 단의 계산이 복잡한데 Divergence function이 위에서 말했듯이 평균과 표준편차가 얽혀있는 복잡한 함수이기 때문이다.

앞단부터 살펴보자

앞단은 상대적으로 계산이 쉽다. 그다음단은 아래와 같다. 

마지막 단은 아래와 같다. 우선 평균이 u와 표준편차에 모두 걸려있어서 두개에 대한 미분을 진행해야 한다. 

위의 과정을 정리하면 아래와 같다. 

test 과정에서는 만약 batch 상태로 온다면 그냥 그것의 평균과 분산값을 구하면 되지만 실제로는 통째로 들어오지는 않는다. 그래서 주로 running average를 많이 사용한다. 그것은 아래와 같다.

여기서 표준편차에 B/(B-1)은 unbiased estimator를 나타낸다. 

결론적으로 batch normalization은 모든 layer에서 사용안하고 어떤 layer에만 사용하여도 되며 convergence rate와 performance에 좋은 효과를 보인다. 

 

Overfitting

위의 경우에서 우리는 파란색의 함수를 원하지 보라색의 형태를 원하지 않는다. 보라색이 나온 경우는 모델에 제약을 두지 않아서 이다. 뉴럴 네트워크에서 각각의 퍼셉트론은 각각의 activation을 거쳐 output이 나온다. activation에 들어가기전에 weighted sum을 하는데 이때가 문제이다. sigmoid를 예를 들어보면 

위에서 weight가 커지면 커질수록 함수가 가팔라지는 것을 볼 수 있다. 이는 sigmoid함수는 양끝은 완벽히 0또는 1임으로 시그모이드에 들어오는 수가 커지면 1밖에 못나타내기 떄문이다. 빨간색같은 함수가 형성되면 data들은 정확이 0또는 1로 구분되어 위의 보라색 함수가 형성되는 것이다. 그래서 weight의 크기를 제한해야 output이 smooth해진다. 그 제약은 아래와 같이 한다. weight의 norm에 기반을 한다. 

여기서 감마값은 weight값을 얼마나 유지할지를 결정해준다. 감마값이 커면 weight를 더 줄어들게 하는셈이다. 

 

또한 깊게 layer를 쌓을 수록 네트워크가 좀더 smooth해진다. 

 

또한 drop out도 위의 문제를 막을 수 있는 좋은 방법이다. 이는 논문리뷰에 올려놓은 것을 보면 알 수 있다. 

 

elephant-is-elephant.tistory.com/3

Dropout : A Simple Way to Prevent Neural Network from Overfitting