2020. 12. 29. 11:47ㆍ논문 정리
1. Introduction
제한이 없는 상황에서는 규정된 모델을 regularize하는 가장 좋은 방법은 모든 파라미터들을 가용하여 계산하는 것이다. 이때 나오는 오차를 Bayesian gold standard라고 한다. 그리고 우리가 딥러닝으로 구현한 것은 최대한 이 Bayesian gold standard에 근접하는 모델을 만드는 것을 목적으로 한다.
하지만 이렇게 만드는 것은 많은 제약이 따른다. 우선 많은 separately trained nets를 계산하는 것은 비용이 많이 들고 많은 architecture들을 훈련시키는 것도 그것에 맞는 hyperparameter를 찾아야하고 많은 데이터도 필요하고 많은 계산 또한 필요하기에 힘들다.
Dropout은 위에 이슈들을 어느정도 해결해준다. 과적합을 줄여주고 많은 neural network architecutre들을 효과적으로 다룰 수 있게 해준다. Dropout은 말그대로 각각의 unit(node)를 랜덤하게 제거하는 것이다.

위의 사진에서 (b)가 drop out이 된 후의 상황을 이야기 한다. 그리고 이때의 network를 thinned network라고 하고 thinned network는 dropout에서 살아남은 unit들로 구성된 network를 이야기 한다.
n개의 unit이 있다면 thinned network가 구성되는 종류는 총 개의 경우의 수가 나온다. 각각의 training case에서 새로운 thinned network가 형성 됨으로 결과적으로
개의 thinned network를 학습하는 것과 같다.
하지만 test time에서는 train set에서 했던 network가 계속 달라짐으로 결과를 평균내는 것은 쉬운 일이 아니다. 그래서 test time에서는 single neural net을 drop out 없이 사용한다. training때 unit이 p의 확률로 존재했다면 test time에서는 weight에 p를 곱해서 계산을 한다. 이 방법으로 hidden unit의 expected output이 test 때의 실제 output과 같아진다.

Dropout은 feed-forward neural network에만 제한적으로 할 수 있는 것이 아니다. 볼츠만 머신에서도 적용 될 수 도 있다. 이는 후에 서술 될 예정이다.
2. Motivation
Dropout은 생식에서 아이디어를 얻었다. 유성 생식은 양 부모에서 반반의 유전 정보와 약간의 random noise로 이루어진다. 이에 반해 무성 생식은 자기의 유전자를 자식에게 거의 그대로 가져다 준다. 언뜻 보면 무성 생식이 자기의 최고의 유전자만 자식에게 가져다 주기 때문에 더 유리하다고 볼 수 있지만 유성 생식도 그 나름의 강점이 있다. 유전자는 자기 것 이외의 랜덤한 유전자와 섞였을 때 더 강화가 된다. 그래서 유성 생식은 이러한 강점을 잘 살릴 수 있다는 점이 있다. 위와 같은 원리로 이것을 뉴런 네트워크로 가져 오면 다음 단의 유닛을 랜덤으로 정했을 때 좀더 효과적인 결과가 나올 수 있다고 생각되었다.
4. Model Description
L개의 hidden layer가 있고 l은 L개의 hidden layer중 하나라고 하자. 그리고 그 l번째 layer에서 input vector를 이라고 하고 output vector를
, weight와 bias를 각각
로 한다. 그러면 feed forward operation(순전파)는 아래와 같아진다.
여기서 f는 시그모이드, ReLU같은 activation function이다.
여기서 Dropout과정을 추가하면 아래와 같아진다.

Bernoulli(p)는 베르누이 이항 분포이다. 어느 하나가 선택 될 확률이 p라면 선택되지 않을 확률은 1-p인 셈이다.
는 drop out된 결과이다. thinned output이라고 한다. *는 여기서 element wise product이며 각 요소 끼리 곱한 것을 의미한다.
Test과정은 dropout을 사용하지 않고 weight에 확률 p를 곱해서 진행하면 된다.

5. Learning Dropout Nets
SGD를 이용하여 일반 뉴럴 네트워크처럼 학습을 시키면 된다. 다만 각 미니 배치마다 dropout으로 인하여 thinned network가 다름으로 그 때의 network에 맞추어 SGD를 이용하면 된다. 이때 gradient를 0으로 만드는 것이 최종 목표인데 모멘텀, L2 weight decay같은 방법을 같이 사용하면 된다. 특히 max norm regularization이 같이 사용하였을 떄 효과가 가장 좋았다. 이 방법은 weight vector의 크기를 정해진 값보다 작게 유지 시키는 방법이다. 이게 가장 효과가 좋은 이유는 대략적으로 볼의 크기를 정해놓고 그 볼에 가장 깊숙한 곳으로 간다고 할때 dropout이 준 noise로 dropout이 없을 때보다 더 랜덤하게 안가본 곳을 지나가면서 깊숙한 곳으로 갈 수 있기 때문이다.
7. Salient Features
1) Effect on Features
일반적인 뉴럴 네트워크에서 derivative는 각 파라미터에서 계산 되어 loss function을 줄이는 방향으로 나아가게 한다. 따라서 이것은 다른 unit들로 부터 정보를 받아 실수를 줄여나가는 과정인 것이다. 여기서 입력과 출력의 연결 강도가 같아지면 업데이트가 잘 안되게 되고 그 데이터에만 적용이 되는 overfitting이 발생하게 된다. 그리고 처음 보는 data에는 제대로 작동하지 않게 된다. 하지만 dropout은 co-adaptation을 방지하여 다른 hidden unit들을 서로 unreliable하게 만든다. 다른 unit들을 신뢰할 수 없음으로 다른 unit에서 전달된 정보를 통해 오차를 줄일 수 없는 것이다. 아래는 MNIST를 single layer로 학습한 과정이다.

(a)는 dropout이 없이 학습을 시켰는데 co-adapted를 가지고 있고 의미있는 feature를 잡아내지 못하였다. 반면 (b)는 dropout을 사용하였고 이 dropout이 co-adpated를 끊어서 좀더 의미있는 결과(edge, stroke)등을 찾아 낼 수 있었다.
2)Effect on Sparsity - sparse model이 좋은거?
dropout의 부작용은 hidden unit의 활성화가 sparse해진다는 것이다. 좋은 sparse model에서는 어떤 데이터든지 few highly activated units여야하고 activation의 average가 낮아야 한다.

위의 히스토그램은 왼쪽은 hidden unit들의 mean activation을 나타내고 오른쪽은 hidden units들의 activation 분포를 나타낸다. (b)가 더 적은 hidden unit들이 활서오하 되었고 평균 또한 낮았다.
3)Effect of Dropout Rate
이 논문에서는 두가지 실험을 하였다. 첫번쨰 실험은 hidden unit의 갯수를 일정하게 유지 시키고 dropout rate(p)만 변화시키는 것이였다. 이 결과 p가 증가할수록 에러는 감소하는 것을 볼 수 있었다.

두번째 실험은 pn을 일정하게 유지 시키는 것이다. 예를들어 hidden unit갯수인 n이 커지면 dropout rate(p)를 낮추는 식이다. 이 실험에서 p가 작을때 유의미한 결과를 얻었는데 위에서의 실험보다 에러가 더 작았다. 하지만 usual default value인 p=0.5일때는 optimal하지 않았다.

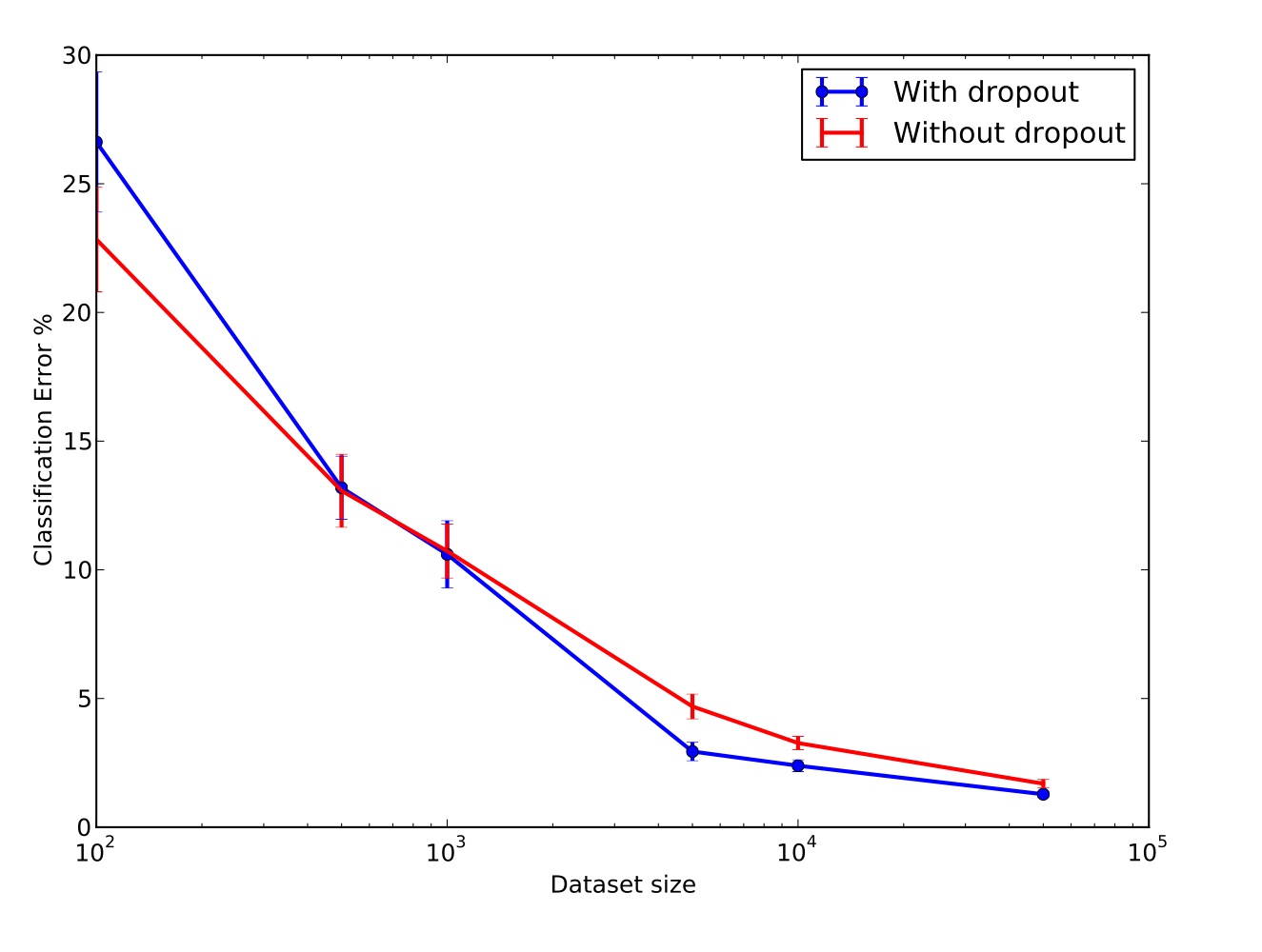
4)Effect of Data Set Size
좋은 regularizer는 적은 data set을 많은 parameter를 이용해 훈련할때 좋은 generalization error가 나와야 한다. 하지만 dropout은 적은 dataset에서 유의미한 결과를 내지 못하였다. model이 충분한 parameter를 가진다면 dropout이 생성하는 noise로도 overfitting을 억제할 수 없는 것이다. 따라서 data의 수에는 "sweet spot"이 있고 이 적정선을 지켜야 유의미한 결과를 낼 수 있다.
5) Monte-Carlo Model Averaging vs Weight Scaling
논문에서는 테스트를 할때에는 dropout을 하지않고 각 weight를 scaling down을 하여 prediction을 하라고 하였다. 그리고 이것을 Approximate averaging이라고 한다. 하지만 좀더 정확한 방법은 각 test case에서도 k번 dropout을 적용하여 그 때 나온 결과를 평균을 내는 것이다. 이를 Monte-Carlo Model Averaging이라고 하고 이때 k가 무한에 다가간다면 실제의 값과 같아질 것이다.
이 논문에서는 k의 갯수를 늘려가면서 실험을 해보았고 k가 작을때는 에러률이 컸지만 k가 점점 커지면서 점점 appriximate방법의 결과에 다가가는 것을 확인할 수 있었다(k=50 일때). 따라서 이는 weight scailing으로 test하는 것이 true modeling의 결과에 가장 가깝다고 할 수 있다.
'논문 정리' 카테고리의 다른 글
| You Only Look Once: Unified, Real-Time Object Detection (0) | 2021.02.26 |
|---|---|
| Training Region-based Object Detectors with Online Hard Example Mining (0) | 2021.02.24 |
| Faster R-CNN : Towards Real-Time Object Detection with Region Proposal Networks (0) | 2021.02.21 |
| Deep Learning (0) | 2020.12.27 |