2021. 1. 13. 02:03ㆍ딥러닝 강의 정리
Generative model
generative model은 data x를 확률분포(probability distribution)으로 나타낸 모델이다. 몇게의 generative model을 보자면 multinomial PMF와 Gaussian PDF가 있다.
우선 multinomial PMF를 보자면 discrete하기 떄문에 P(x=v)를 P(v)라고 한다.

Gaussian PDF는 아래와 같이 정의된다.
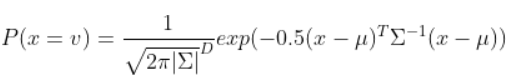
여기서 μ는 평균을 의미하고 Σ는 분산을 의미한다.

generative model을 배운다는 것은 X={x}라는 observed data가 주어지면 P(x;θ)의(여기서 θ는 모델에 대한 parameter이다.) x에 대한 distribution model을 선택하여 그 X set에 가장 잘맞는 θ를 찾는 것이다. 예를들어

왼쪽이 observation일때 우리는 Gaussian model을 정해야한다. 이때 평균과 분산을 이용해 정한다. 그리고 오른쪽 그림처럼 어떤것이 best fit인지를 찾는 것이다. 여기서 best fit이란 data가 있는 곳에서 highest probability를 가지는 것을 의미한다. 즉 data가 많이 나오면 probability가 높고 적게나오면 그곳은 probability가 낮은 식이다.
Likelihood는 지금 얻은 데이터가 이 분포로 부터 나왔을 가능도를 이야기하는데 Maximum likelihood는 이것의 최대값을 의미한다. . 를 의미하는데 보통은 여기에 이렇게
log를 붙여 사용한다. 그리고 이 가능도는 각 데이터 샘플에서 후보 분포에 대한 높이를 계산해서 다 곱한 것이다. 예를들어보면 아래의 히스토그램에서는
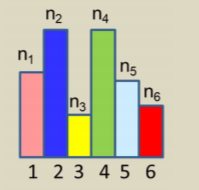
인데 여기서 P(x)를 직접대입하면
이다. 여기서 product를 log의 성질을 이용해 summation으로 바꾸면
로 나타낼 수 있다. 가우시안도 마찬가지 방법으로 아래처럼 나타낼 수 있다.
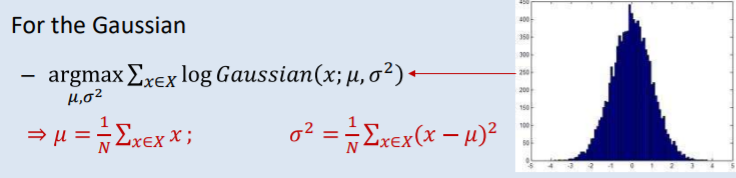
Incomplete Data
하지만 이렇게 계산하는 것은 모든 데이터를 완벽히 알때이고 때로는 데이터가 불완전하게 들어올 때가 있다. 그것에는 여러가지 이유가 있는데 우선 데이터 자체가 missing component를 가지고 있을 때를 보자.

위의 데이터에 대한 maximum likelihood를 계산하려고 아래의 식을 사용했다.
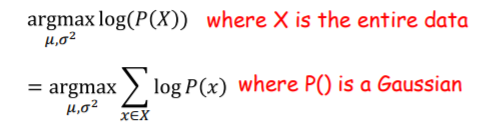
하지만 이때 P(X)에서 X는 data전체를 이야기하는 것이고 이는 곧 missing data가 있으면 안된다는 것을 의미한다. 그래서 위의 데이터를 두부분으로 나누었다.

위처럼 제대로 들어온 data를 observed data로 O라고 표현하고(O={O1,O2,,,,}),

위처럼 빠진 data를 missing data라고 m이라고 표현한다.(M={m1,m2,,,,})

위의 complete data를 X={x1,x2,,,,}라고 할때 각각의 xi는 Oi와 mi를 포함한 이다. missing data는 아예모름으로 그나마 알고있는 observed data로만 maximum likelihood를 계산하려고한다. 그 식은 아래와 같다.
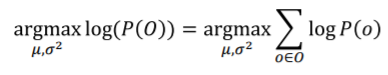
그런데 여기서 P(o)역시 결국 P(x)를 알아야 하기에 전체의 데이터가 필요하다. 그래서 이방법도 사용할 수 없다.
P(x)를 o와 m을 이용해 joint probability로 P(x)=P(o,m)으로 나타내보면 이를 이용해 P(o)를 구할 수 있다.

그러면 전체 observed data의 log probability는 아래와 같게 된다.

여기에 argmax를 붙이면 우리가 구하고자하는 obsereved data로만 maximum likelihood를 계산한 결과가 나온다.

하지만 log of integral은 closed form이 아니여서 계산을 못하는 경우도 생긴다.
또다른 incomplete data 생성의 이유로 네트워크의 구조적 문제가 있다.

이 generative model은 data를 두가지 단계로 생성한다. 우선 Gaussian을 P(k)의 확률로 선택한뒤에 그 고른 모델에서 vector o를 뽑아내는 것이다. 이러한 모델을 mixture gaussian이라고 한다. 이 모델의 목표는 모든 training data의 gaussian 파라미터를 배우는 것이다. 또한 gaussian이 뽑히는 확률도 배우게 된다.
따라서 이 프로세스에는 2개의 변수가 존재하는데 하나는 k이고 다른 하나는 o이다. 그래서 각각의 draw의 확률은 아래와 같이 joint probability로 나타내 진다.

이를 이용해 observation o의 확률을 구하면 아래와 같다.

여기서의 complete data는 data vector o와 gaussian을 뽑을 확률인 k이다.

그리고 그 gaussian을 바탕으로 각각을 분리해서 평균과 분산을 계산하는 것이다.

하지만 우리는 각 observation마다 실제 gaussian이 뭔지를 모른다. 따라서 incomplete한 data를 받게 되는 것이다. 마찬가지로 여기에서 observed data만 이용해서 Maximum liklihood를 계산해보자.

위의 식에 아까 P(o)를 구했음으로

이 둘을 결합하면 아래의 식을 얻을 수 있다.

하지만 log of sum은 아까 설명처럼 계산이 항상 되지 않는다.
결론적으로 incomplete data에 대한 maximum likelihood를 계산하는 두가지방법을 일반적으로 표현하면 아래와 같다.

EM
log of sum때문에 계산이 힘들었는데 이를 어떻게 해결할 수있을까?
우선 incomplete data에 의한 문제를 해결해보자.

위의 data vector는 수많은 벡터중에 하나를 뽑은 것이다. 그리고 우리는 저 missing 부분을 채워놓아서 obaserved componete와 match 시키려고 한다. 아무거나 넣는 것이 아닌 data distribution을 통해 observed data와 어울리는 것을 넣는 것이다. 물론 굉장히 많은 data가 들어갈 수 있다. 그래서 이를 조건부 확률을 이용해 P(m|o)로 표현한다. 이는 observed data중 m을 고를 확률을 의미한다. 이를 위해 아래처럼

그 하나의 data를 복제해서 모든 가능한 값을 넣는 것이다. 그리고 각각에 P(m|o)라는 비율을 넣는다. 이를 모든 데이터에 대해 하는 것이다.

그 과정은 다음과 같다. 우선 위처럼 expanded set을 만든다. x_i(m)을 o_i observation에 m이라는 missing component를 넣어 complete data를 만든 것이라고 하자. 즉,인 것이다. 그리고 이 x를 통해 평균과 분산을 구한다.
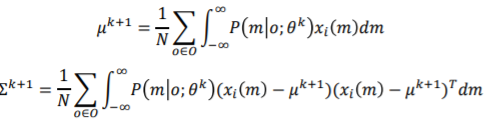
평균에서 은 i번째 expanded set에서의 proportional sum을 의미한다.그리고
는 k번째 평균과 분산 parameter를 의미한다. 이를 converge할때까지 반복하는 것이다.

이번에는 data structure의 문제로 생긴 incomplete data를 해결해보자. 여기서도 마찬가지로 single vector를 생각해본다.

그리고 이것을 모든 gaussian에 대해 expand한다.

그리고 각각이 생성될 확률을 P(k|o)로 둔다. 위의 경우 gaussian이 3개임으로 아래처럼 3개로 둘 수 있는 것이다.

그리고 각각의 data를 위와 같은 방법으로 expand한다.
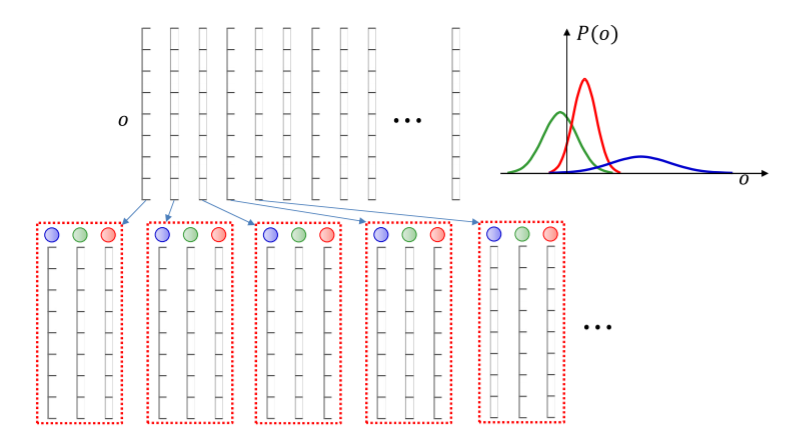
이렇게 두면 각각의 Gaussian에 대해 complete vector를 만들 수 있는 것이다. 그 뒤 각각의 vector를 Gaussian에 따라 분류한다.

그리고 위에서 blue gaussian, green gaussian, red gaussian에 따라서 평균과 분산을 계산하는 것이다.

여기서 는 k는 고정되어있고 data만 바뀐다. 즉 k는 파란색, 초록색, 빨간색 이렇게 따로 구한다는 것이다.
위에서의 과정을 Estimation Maximum(EM)이라고 부른다. 이 방법은 일반화하자면 우선 missing data를 complete data로 바꾸는데 이때 clone을 만드는 sampling 과정을 거치고 이 각각에 sample에 P(m|o), P(k|o)같은 proportion을 넣어서 계산해주면 되는 것이다.
PCA
이제 Principa Component Analysis(PCA)를 살펴보자. 아래의 데이터가 zero mean data라고 가정해보자.

PCA란 모든 벡터들이 principal subspace에 들어있는 subspace를 찾는 것인데 이때 approximaiton eroor가 가장 작은 subspcae를 찾는 것을 의미한다.

두가지 방법으로 구할 수 있는데 우선 closed form을 살펴보면 아래와 같이 수학적 계산으로 풀 수 있다.



이것은 데이터가 커지면 계산이 힘들어진다는 단점이 있다. 이번에는 iterative한 방법으로 구해보자.

우리의 목적은 vector w와 position vector z를 찾아 zw가 최대한 x와 같게만드는 것이다. X=[x1,x2,x3...,xn]이라고 하자. 우선 아래와 같이 subspace를 initialize한다.

그다음 각각의 training data에 대한 가장 best인 position vector z를 찾아야하는데 subspcae에 projection된 점을 찾는다. 그리고 그 좌표가 z이다.

이 position vector를 유지한채로 subspcae를 회전시킨다. 최대한 training data와 projection된 것의 거리가 가깝게 만든다.

그다음 다시 그 subspace에 training data를 projection시킨다.

그리고 다시 돌리고 projection하고를 converge할때까지 진행한다.


위의 과정을 간단한 다이어그램으로 나타내면 아래와 같다.

1. 주어진 W에 대해 best position vector z를 찾는다. 이것을 수식으로 나타내면 이다. 여기서
의 의미는 pseudo inverse를 의미한다.
2. 위에서 정한 z에 대하여 best subspace를 찾는다. 이것을 수식으로 나타내면 이다.
여기서 1이 파란색 박스부분이고 2가 노란색 박스부분인것이다.
위를 한줄로 나타내면

인데 이것은 autoencoder와 모습이 유사하다. 파란색 부분이 encoder부분이고 노란색이 decoder부분인 것이다.
여기서 한가지 문제점이 있는데

위의 그림처럼 같은 subspcae에서 w가 달라질때마다 position vector z가 달라지는 것이다. 즉 z가 일정해야 하는데 계속 변하는 것이다. 따라서 이를 위해 두가지 방법이 있다. 하나는 W의 벡터를 unit length와 orthogonal로 만드는 것이고 다른 하나는 z의 distribution을 standard Gaussian으로 정하는 것이다. 두번째 방법에 집중해보자.

위의 형태로 만들어야 하는 것이다. 어떻게 해야할까? 이를 위해 우리가 위에서한 iterative solution을 다시 살펴보자.
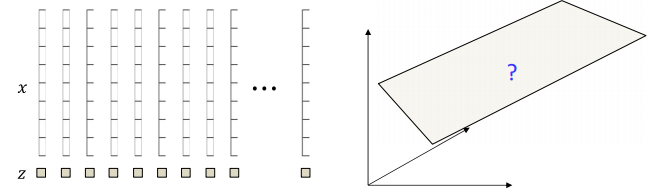
각각의 벡터 x에 대하여 여기서 우리는 z즉 position vector의 정보를 가지고 있지 않다. 이 z가 missing data인 것이다. 만약 여기서 z를 알고 있다면 바로 subplane을 계산할 수 있을 것이다. 이를 위해 우리는 먼저 plane을 initialize했다.

그다음 그 plane에 알맞는 z를 찾아서 complete data를 만들었다.

이제 complete data를 가지고 있으니 이를 이용해 다시 plane을 재조정하였다.

이 과정을 계속 반복한 것이다. 이것은 위에서 우리가 본 EM과 같다. EM에서는 generative model이 필요한데 여기서 z를 standard Gaussian으로 넣은것이다.
따라서 Autoencoder를 아래처럼 설계할 수 있는 것이다.

Generative story behind PCA

어떠한 point를 생성하려면 먼저 principal plane에서 Gaussian step을 밟은 뒤에 거기서 orthogonal Gaussian step을 밟는다. 이것으로 데이터를 다시 생성하는 것이다. 자세히 살펴보면

위와 같은데 z는 principal plane의 차원을 가지고 있는 Gaussian이고 여기에 Az를 가해서 구하고자하는 데이터의 projection위치로 간다. 여기서 A는 'basis' of subspace matrix인데 principal eigen vector로 이루어진 matrix에 eigen value를 곱한것이다. 그리고 E는 그 principal subspace에 orthogonal한 Gaussian noise이다.
따라서 PCA는 X를 training하면서 A와 D의 정보를 얻는 것이다.
이를 AutoEncoder의 관점에서 바라보자.

decoder에서 data를 생성하는 것이다. 이때 decoder의 weight는 그냥 PCA basis matrix가 된다. encoder 부분까지 보면

encoder는 그냥 standard Gaussian에 projection하는 것이고 decoder는 PCA basis matrix를 weight로 가져 data를 생성하는 것이다.
그리고 여기에 noise를 더하는 것은

z가 Gaussian이면 X hat도 Gaussian이고 E도 Gaussian임으로 X도 Gaussian으로 나온다. 그래서 오른쪽의 분포가 PCA가 사실상 만드는 것이다.
하지만 항상 principal subspace와 노이즈가 orthogonal하지는 않다. 예를들어 노이즈를 사진에 넣어도 사진이 제대로 보인다. 때문에 noise를 아무 방향으로 해도 되게 한다.

full rank Gaussian uncorrelated noise를 넣는데 여기서 Uncorrelated는 diagonal covariance matrix를 의미한다.

위에처럼 데이터가 어디에서 오는지 이제 몰라서 확률로 표시해야 한다. 이떄 확률은 A와 D로 나타낼 수 있다.
이 자료는 제가 강의들은 것을 바탕으로 복습겸 정리한 것입니다. 틀린부분이있으면 지적해주세요!
출처: www.youtube.com/watch?v=oMWwn_RSQzQ&list=PLp-0K3kfddPzCnS4CqKphh-zT3aDwybDe&index=29&t=2981s
'딥러닝 강의 정리' 카테고리의 다른 글
| Hopfield Nets and Boltzmann Machines/Lec.17 (0) | 2021.01.12 |
|---|---|
| Hopfield Nets and Boltzmann Machines/Lec.16 (0) | 2021.01.12 |
| Hopfield Nets and Auto Associators/Lec.15 (0) | 2021.01.11 |
| Representation/Lec.14 (0) | 2021.01.09 |
| Sequence to Sequence Models : Attention Models /Lec 13. (0) | 2021.01.08 |