2021. 1. 12. 19:39ㆍ딥러닝 강의 정리
Problem with Hopfield Network
지금까지본 hopfield network의 단점은

위에처럼 recall을하는데 원본과 완벽하게 똑같이 나오지 않는다는 것이다.

이것은 위처럼 parasitic memory가 생겨나기 때문이다. 저기도 minima이기때문에 evolve도중 저기에 갇혀버려서 나올 수 없어 위처럼 노이즈가 발생한다. 그래서 이것을 해결하기 위해서는 저기에 갇히는 것을 방지해야 한다. 그릴 위해서 원래 flip할때 에너지가 줄어드는 것만 형태만 받아들였는데 이제는 약간 증가해도 그 state를 가져가기로 한다.
Spin Galsses를 다시 살펴보자.

diapole은 위의 관계들을 가지며 에너지가 어떠한 local value에 converge할때까지 계속 변하게 된다. 그 부분이 stable configuration인 것이다. 여기서 물리학적 사실을 다시 생각해보자. system은 어떠한 상태에서 딱 한 state만 가지고 있을까? 그것은 사실 아니다. state는 sytme의 온도에 따라서 continuously changing을 한다. 예를들어 온도가 높다면 state는 좀더 빠르게 chaginge되는 것이다. 그리고 state를 같은 조건에 그 state에 있을 확률로 표현한다.
T 온도에서 어떠한 시스템이 state s에서 발견될 확률이 라고 하자. 그리고 각각의 state s에서의 potential energy는
라고 한다. 그러면 시스템의 internal energy, 즉 일을 할수 있는 용량은 아래와 같이 평균으로 나타낼 수 있다.

그런데 그 흐름을 방행하는 엔트로피같은 것도 있다. 이는 internal disorder of the systme이라고 한다. 그 식은 아래와 같다.

이 둘을 합친 것을 Helmholtz free energy of the system이라고 하는데 useful work를 얼만큼할 수 있는지 알려준다.

steady states에서의 확률분포를 Boltzmann distribution이라고 한다. 위 식에서 internal disorder of the system 식에 kT가 곱해져 있는데 이는 온도가 높을 수록 일을 하는 것을 방해한다는 것을 이야기한다. 시스템은 상태가 계속 변하면서 free energy를 줄이는 방향으로 나아간다. 그럼 어디까지 나아가는 것일까? free energy의 최솟값을 구하기 위해 위의 식을 미분해보자.

이렇게 system이 minimum에 가면 Probalility distribution over the state를 구할 수 있다. 이를 Gibbs distribution이라고 한다. Z는 normalizing을 위해 넣은 것이고 이것은 온도에 dependent하다. 그리고 만일 온도가 0이라면 이 시스템은 항상 lowest energy configuration을 가지고 있을 것이다.
위에서 보았듯이 system의 evolution은 사실 확률적인 것이다. 그리고 그 어떠한 state에 있을 확률은 에너지와 온도와 관련이 있다.

여기서 E가 0일때 P(s)가 가장 크고 E가 커질 수 록 P(s)가 줄어든다. 이는 에너지가 줄어드는 상태를 지향하는 것을 의미한다.
위에서 밝힌 내용을 다시 hopfield로 가지고 와보자. 에너지는 아래와 같이 쓸 수 있다.

이를 P(s), 즉 확률로 나타낸다면 아래처럼 softmax형식으로 나타낼 수 있는것이다.

single node에서 예를 하나 들어보자. i번째 비트에서 S와 S'라는 상태가 있고 S일때는 i번째 bit가 +1이고 S'일때는 -1이라고 해보자. 그러면 각각의 S와 S'에 대한 확률은 아래처럼 나타낼 수 있다. S상태라는 것은 n개의 비트 상태중에 s_i=1일떄니깐 이것은 이므로 베이스룰에 의하여
이다. S'도 역시
이다. 이 두상태의 확률의 차에 log를 씌우면 아래의 식을 구할 수 있다.
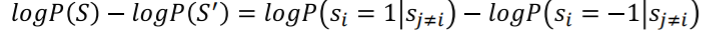
그런데 어차피 P(S)=1-P(S')임으로


즉 field of current node가 나오게 된다. 따라서 이는

위의 식이라는 것이고 여기서 P만 따로 뺴내면 아래의 식을 얻을 수 있다.

이것은 어떠한 node가 1을 가질 확률은 sigmoid, 즉 logistic function으로 표현된다는 것이다.
이제 이 네트워크를 위의 정보를 토대로 다시 재구성해보자. 그러면 아래의 식들을 가지게 된다.

각각의 뉴런은 stochastic unit이 되고 각각의 binary state s는 0또는 1을 가지게 되는데 그 확률은 local filed의 계산 값을 sigmoid에 넣음으로서 알 수 있다. 이렇게 Hopfiled network를 boltzmann distribution을 이용하여 얻을 수 있는 것이다.
여기에 위의 spin glasses에서 배운 temparature의 개념까지 넣어보자. 넣은 결과는 아래와 같다.

z에 temparature을 나누어준 것이다. 이렇게되면 high temarature에서는 지금 상태가 global minimum이여도 z가 0에 가깝기 때문에 P가 0.5가 되고 flip할 확률이 커지게 되는 것이다. 그래서 이런식으로 위에서 parasitic memory의 local minimum을 탈출 할 수 있는 것이다. 여기서 T가 0이라면 위에 spin glasses에서 본 것 처럼 항상 lowest configuration을 가지려고 하고 이것은 결국 deterministic Hopfield behavior가 되는 것이다.
위를 이용한 local minima를 빠져나가는 방법은 다음과 같다. 우선 initial pattern으로 initialize network를 한다.

그다음 몇개의 iteration을 정하는데 예를들어 y0,y1,....,yL의 sequence를 정한뒤 evolve를 진행한다. 그리고 그 결과를 평균을 내어 만일 그것이 0.5보다 크다면 output을 1로 둔다. 이 과정을 temparature가 T_min까지 될때까지 진행하는 것이다.

위의 방법을 이용해 local minima를 빠져나가 제대로된 원본을 구할 수 있는 것이다.
The Boltzmann Machine
위에서 어떠한 state가 될 확률을 보았다.

이를 이용해 Boltzmann distribution을 가지고 아무 y state가 될 확률을 구할 수 있다.

그리고 이를 이용한 네트워크를 Boltzmann Machine이라고 한다.
이제 네트워크 training하는 것을 보자. 앞에서 배운 Hopfiled Network의 training은 기억해야할 target state를 기억하지 않을 state와 구분하는 weight를 구하는 것이였다. Boltmann Machine도 비슷한데 여기선느 probability를 이용함으로 기억하고 싶은 패턴에는 high probability를 부여하고 아닌 것에는 low probabiltiy를 부여하는 weight를 찾는 것이다. 즉 기억할 stored states의 가능성을 최대로 만들어야 하는 것이다.
우선 P(S)는 아래처럼 정의할 수 있다.

여기에 E를 대입하면 아래를 얻을 수 있다.

여기에 log를 붙이면 아래를 얻는다.

여기서 training vector들에 대한 가능도들의 평균은 아래와 같다.

위의 각각의 vector에 대한 log(P(S))의 합을 trainig vector의 수로 나눈 것인데 log(P(S))에서 두번째 항이 S와 관련된 함수가 아님으로 아래와 같이 나타낼 수 있다.

이것을 maximize하는 것이 우리의 목표이다. 그를 위해 w로 미분을 해보자. 우성 첫번째 항의 미분은 아래와 같다.부분은 지금 각각의 w에대해 미분한 것임으로 사라지게 된다.

두번째항을 미분하면 아래와 같다.


그냥 모든 possible value of state에 대한 si,sj의 기댓값인 것이다. 이는 모든 state에 대한 것임으로 현실적으로 계산이 불가능하다. 그래서 아래처럼 sampling을 통해 계산을 진행한다.

그렇다면 이 sample은 어떻게 얻을 수 있을까? 우선 네트워크를 랜덤하게 initialize한 후 evolve시킨다. 많은 evolution 후 그 state들을 뽑아낸다. 이를 계속 반복하면 아래와 같은 sample을 얻을 수 있다.

위에 첫번째 항과 두번째항의 미분값을 합치면 아래의 결과를 얻을 수 있다.

그리고 이것을 maximize 방향으로 보내야 함으로 gradient asccent를 이용한다.

아래는 hopfield network의 update인데 Boltzmann과 굉장히 유사한 것을 볼 수 있다.

Increase Capacity
지금까지는 N개의 뉴런이 있다면 N개의 패턴까지만 기억할 수 있었다. 그렇다면 이 용량을 늘리는 방법은 없을까? 이를 위해 N보다 큰 K개의 뉴런을 가져온다. 다만 이 K개의 뉴런은 우리가 실질적으로 상관하지 않는 뉴런들이다.

이렇게 되면 N+K개의 뉴런을 기록할 수 있다. 여기서 우리가 실질적으로 패턴을 저장하는 뉴런을 visible neuron이라고 하고 용량 늘리기위해 추가한 뉴런을 hidden neuron이라고 한다.
이렇게 hidden neuron을 연결하게 되면 주어진 visible neuron에 대하여 굉장히 많은 hiddend neuron의 패턴이 생겨난다. 그리고 여기서 우리는 lowest energy를 찾아야한다. 하지만 이런게 여러개일 수 있다. 그렇다면 어떻게 그 하나를 고를 수 있을까? 우리는 여기서 그 하나를 고르는 것이 아닌 확률을 이용해 모두를 고려하려고 한다.
hidden neuron을 고려한 probability는 아래와 같다.

visible neuron만 고려했을때는 즉 visible neuron들 안에서만 계산이 되었는데 이것이 hidden neuron과 결합이 되어P(S)=P(Visible, Hidden)이 된 것이다. 여기서 P(V)를 구하려면 관련된 hidden state를 다 더하면 P(V)만 남아 그 확률을 구할 수 있다. 그리고 우리는 이 P(V)를 maximize해야한다. 위에 수식을 좀더 자세히 쓰면 아래와 같다. 에너지를 대입한 것이다.

위에 visible neuron만 있을때의 training 방법과 같이 여기서도 P(V)에 log를 붙이고 모든 training vector에 대한 평균을 구한다. 그리고 그 결과는 아래와 같다.

이것을 마찬가지로 각각의 w로 미분을 하면 아래와 같다.

위 수식은 복잡해 보일 수 있는데 첫번째 항은 결국 주어진 visible state에 대한 모든 hidden state들의 expected value이고 두번째항은 모든 state들에 대한 eexpected value이다. 따라서 아래로 정리할 수 있다.

그리고 여기서 sampling을 사용한다. Visible state에 걸린 hidden state는 굉장히 많고 전체 state는 위에서도 말했듯이 수없이 많음으로 아래처럼 각각 sampling을 진행한다.

샘플링하는 법은 다음과 같다. 각각의 training patter Vi에 대하여 우선 이 visible pattern을 고정시킨뒤 이에대해 hidden neuron을 random initial point로부터 evolve시킨다. 그리고 이 결과로 Hi를 뽑는다. 이 두개를 결합해 Simulation Si=[Vi, Hi]로 둔다. 이렇게 한개의 training pattern으로 부터 여러개의 샘플을 뽑아내고 이를 모든 training pattern으로부터 얻어냄을서 아래와 같은 Simulation set를 만들어 낸다. 이를 clamping 시킨다고 한다.

두번째로 이제 고정시킨것을 풀고 모든 네트워크에 대하여 evolve를 시킨다. 이 결과를 아래처럼 나타낼 수 있다.

그리고 이 두 결과를 clamp한 것을 첫번째 항에, unclamp한 것을 두번쨰 항에 넣어 미분을 진행하면 된다.

그리고 이 미분 결과를 gradient accsent를 위해 아래처럼 update한다.

이 Boltzmann machine을 classification에도 사용할 수 있는데 one-hot vector를 하나의 training pattern으로 생각하고 같은 방식으로 훈련시킨뒤에 각각의 class에 대한 조건부확률을 구하면 된다.
Restricted Boltzmann Machine
위의 Boltzmann Machine의 단점은 너무 오랜시간이 걸리고 large problem에는 적합하지 않다는 것이다. 그래서 이를 해결하기 위하여 아래처럼 fully connected가 아닌 MLP같은 느낌으로 만든 것을 restricted boltzmann machine이라고 한다.
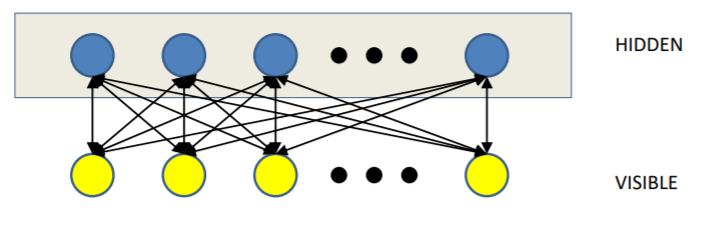
Visible unit은 오직 hidden unit과만 연결되고 다른 visible unit과는 연결이 안된다. hidden unit도 마찬가지이다. 하지만 여전히 위에서 배운 Boltzmann machine의 방식을 그대로 따른다.

하지만 이렇게 구조를 만듦으로서 굉장한 이점이 생기는데 전에 boltzmann에서는 하나의 visible pattern에 대해서 여러번의 evolve를 거쳐서 샘플을 만들었는데 restricted boltzmann에서는 하나의 visible pattern에 대해 한번만 샘플링을 하면 된다. 그리고 거기서 나온 샘플링을 다시 이용해 visible sample을 만든다.

여기서 P(v)는 Boltzmann에서

이렇게 주어진 visible state에 대한 모든 hidden state들의 expected value에서 모든 state들에 대한 eexpected value를 뺸 값으로 구했는데 여기도 마찬가지다. 다만 위에서 말했듯이 여러개의 hidden state를 구할 필요없이 한번만 구하면 되기에 첫번째항은 저 식에서 부분이 빠지게되는것이고 전체 state에 대한 expected value는 위의 그림에서 화살표를 따라서 계산하다 무한번쨰에서의 state임으로 무한번 돌리면서 얻은 값들의 exptected value를 구하면 된다.
현실적으로 무한번 돌리기는 어려운데 한번만 돌려도 충분하다는 연구결과가 있다. 그래서

이렇게만 돌리고 위와같이 계산하면 충분히 미분값을 구할 수 있다.
(이부분은 강의에서도 설명이 충분하지 않아 angeloyeo.github.io/2020/10/02/RBM.html#boltzmann-machine이 블로그를 참조하면 정말 좋을것 같습니다)
이 자료는 제가 강의들은 것을 바탕으로 복습겸 정리한 것입니다. 틀린부분이있으면 지적해주세요!
www.youtube.com/watch?v=R2sFABfmlXQ&list=PLp-0K3kfddPwz13VqV1PaMXF6V6dYdEsj&index=23
'딥러닝 강의 정리' 카테고리의 다른 글
| Variational Autoencoders/Lec.18 (0) | 2021.01.13 |
|---|---|
| Hopfield Nets and Boltzmann Machines/Lec.16 (0) | 2021.01.12 |
| Hopfield Nets and Auto Associators/Lec.15 (0) | 2021.01.11 |
| Representation/Lec.14 (0) | 2021.01.09 |
| Sequence to Sequence Models : Attention Models /Lec 13. (0) | 2021.01.08 |