Training Neural Networks: Optimization/ Lec6.

Momentum

전 강의에서 RProp과 QucikProp의 단점으로 각 dimension이 independent하게 움직이기 때문에 어느 곳은 converge하고 어느 곳은 diverge해서 결과적으로 계속 왔다갔다하며 oscillating해 제자리에 머무를 수 도 있다고 하였다. 이를 막기 위하여 모멘텀이라는 방법이 나왔다. 이 방법은 전의 모든 step의 값을 평균을 내어 가지고 있는다. 만약 한방향으로 계속 나아간다면 그 평균값은 점점 커질 것이다. 하지만 step과정이 왔다갔다 swing을 한다면 drivative가 양수, 음수 번갈아 나옴으로 평균을 점점 까먹을 것이다. 모멘텀 방법은 바로 그순간의 gradient에 집중하는 것이 아닌 과거의 모든 step이 들어있는 running average에 집중을 한다. 아래 그림을 보자.

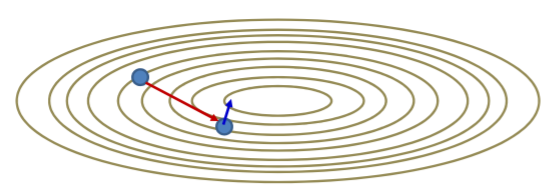
검정색이 첫번째 step라면 그것의 gradient는 수직방향인 파란색 점선 일 것이다. 원래대로라면 우리는 그것의 반대 방향으로 가야됨으로 파란색 실선 방향으로 가야 한다. momentum은 gradient의 평균에 집중한다고 하였다. 수평축의 평균은 분홍색실선이고 수직 축의 평균은 거의 0이 될것이다. 따라서 새로 생성된 두번째 step의 벡터는 분홍색 실선이 된다.  

3번째 step은 아래와 같이 결정될 수 있다. 결론적으로 바로 전 step은 그동안의 평균값을 가지고 있는 셈이고 가로축이든 세로축이든 같은 방향이였다면 average가 점점 커지게 되고 반대방향이면 average가 점점 작아지게 된다. 위를 수학적으로 나타내면 아래와 같다.

단순히 식으로만 보았을때는 빼는 것으로 보이지만 벡터값임으로 벡터의 덧셈,뺄셈은 두 벡터의 평균을 나타내게 된다. 또한 베타는 주로 0.9를 사용한다. 

gradient descent방법과의 차이를 알고리즘을 비교하며 알아보면

gradient descent는 그냥 gradient를 계산한뒤 그 반대방향으로 weight를 업데이트 하는것이다. 하지만 모멘텀은

이부분이라고 써있데 처럼 average를 구한다음 그 것을 이용해 weight를 업데이트 하는 차이가 있다. 

 

모멘턴 방법을 사용하는 순서는 아래와 같다. 

우선 current step을 계산한다. 그 방법은 current location에서의 gradient step을 계산한다음

바로 직전의 step을 scaling 해서 더하면 된다. 

위의 방법도 좋지만 순서를 바꿔서 한다면 더 좋은 방법이 나오게 된다. 이것을 Nestorov's Accelerated Gradient라고 한다. 그 순서는 아래와 같다. 

모멘텀에서는 gradient를 먼저 계산했다면 이번에는 전의 step을 길게 먼저 늘린다. 

그다음 늘린것에서 gradeint step을 구한다. 

그 뒤에서 두개를 더하면 된다. 순서만 달라졌을 뿐인데 모멘텀보다 더 빠르게 converge한다고 한다. 수학적인 수식은 아래와 같다. 

SGD

앞에서 했던 gradient descent는 한번에 주어진 샘플 포인트를 조정한다. 이 행동을 target function과 비슷해질 때 까지 한다. 

파란색이 target function이고 빨간색이 initial function이라고 하자. 그렇다면 초록색 부분은 올려야하고 빨간색부분은 내려야한다. 이것을 한번에 시행한다. 

위의 방법을 Batch Update라고 하며 시행하는 한 묶음의 샘플들을 batch라고 하는데 이것을 한꺼번에 update해서 그렇다. 

 

위와 반대로 샘플을 하나씩 조정하면 어떻게 될까? 아래 그림을 보자.

이렇게 하나씩 조정을 해도 결과적으로는 모든 부분을 조정할 것이며 Batch Update보다 더 결과가 좋다고 한다. 위의 코드는 아래와 같다. 

위에서 T개의 샘플을 t개로 쪼개서 업데이트를 하는데 이때 샘플들 하나하나를 epoch라고 한다. 하지만 위에 코드는 문제가 하나있다. t개로 쪼개진 샘플들을 업데이트 할때 아래 그림처럼 순차적으로 업데이트를 하는 것이다. 

위의 코드대로라면 맨 왼쪽의 epoch부터 조정이 시작된다. 

조정을 하면 그부분만 바뀌는 것이아니라 전체적인 함수가 조금씩 바뀌게 된다. 그래서 맨 오른쪽이 target보다 내려가있었는데 올라가는 경우가 생길 수 도 있다. 

계속 진행하다 오른쪽에 있는 epoch를 조정하려 아래로 내렸더니 

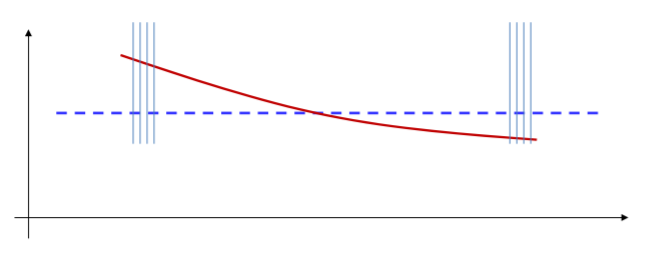
다시 맨 왼쪽 epoch가 위로 올라가는 경우가 생길 수도 있다. 이렇게 cyclic한 성향을 가질 수도 있는 것이다. 그래서 randomly하게 converge하는 성향을 가지게 해야한다. 

위처럼 randomly하게 조정한다면 전반적으로 cyclic한 모양은 없어질 것이다. 이것을 Stochastic Gradient Descent라고 한다. 코드는 아래와 같다. 

epoch들을 하나 하나 조정하기전에 전체적으로 한번 섞어준다. 

 

Batch update와 SGD와 무슨차이점이 있을까? 일반적으로 loss function을 구할때 모든 gradeint의 평균을 이용함으로 loss function의 한점을 잡으면 아래 그림처럼 각각의 component들마다 다른 방향을 가르키고 있을 것이다. 

그렇다면 극단적으로 모든 gradeint들이 같은 방향을 가르키고 있으면 어떻게 될까? 아래 그림처럼 될 것이다. 

위의 상태를 update해나아간다고 하면 Batch update는 모든 점이 같은 방향을 가르키고 있고 한번에 모든점을 update함으로 그 방향 단 한번만 update될 것이다. 하지만 SGD는 각각 따로따로 update함으로 Batch와 다르게 모든 componet들이 계속 update되서 결과적으로는 target function에 더 가까워 질 것이다. 

이러한 성질은 data들이 점점 멀어질때도 그 효과는 줄어들겠지만 어느정도 유지하고 있을 것이다. 

위의 SGD를 좀더 보완해보자. 

만약 위의 빨간 선과 완벽히 일치시키고 싶다고 하면 우리는 절대 위의 코드로 할 수 없을 것이다. learning rate가 고정되어있으면 각 점이 위로 올라가고 내려가는 정도가 항상 같기 때문이다. 그래서 점점 target에 가까워져 갈 수록 learning rate를 줄여나가야 한다. 그것이 아래의 코드이다. 

learning rate에도 함수를 넣어 줄여 나간다. 위의 learning rate들은 전체를 더했을 때 무한대가 나와야 한다. 그래야 모든 parameter space가 사용 될 것이다. 그리고 점점 줄어들어야 함으로 learning rate의 제곱은 무한대보다는 작아야 한다.

위의 조건을 만족하는 함수중 하나가 1/k이다. 그래서 주로 1/k를 많이 사용한다. 

  위는 strongly convex function일때 해당이고 주로 generically convex function에서는 많은 연구에서 가 더 효율적이라는 결과가 나왔다. 

그렇다면 얼마나 빠르게 converge하는 것일까? 우선 converge의 정의를 보면

k번째 iteration에서 우리가 정한 e(입실론)보다 작을 때 converge했다고 본다. k번째는 0번째에서 learning rate를 계속 곱하면서 나온 것이고 그것은 아래와 같다. 

따라서 오른쪽이 e가 나와야함으로 대략적으로  정도의 시간이 걸릴 것이다. Batch update는 learning rate가 고정 되어있음으로 아래와 같다. 

그렇다면 converge하는데 걸리는 시간은 대략 가 걸릴 것이다. SGD가 update 걸리는 시간이 더 느리긴 하지만 SGD는 Batch update보다 더 많은 update를 진행할 것이다. 위에서 보았듯이 Batch는 같은 방향을 가르키고 있으면 한번만 update하기 때문이다. 

 

이번에는 variance의 관점에서 보자. 그전에 예시를 통해 variance의 의미를 알아보자면 

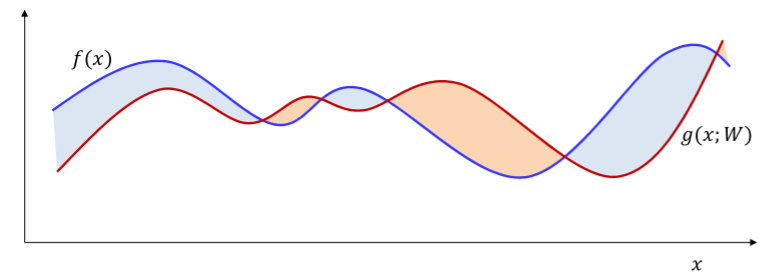
파란색이 target이고 빨간색이 우리가 조정하고자 하는 함수이다. 

색칠되있는 부분이 div이고 우리는 그것의 평균을 이용한다. 하지만 전체의 크기는 알 수 없으니 샘플을 정해서 각각의 샘플에서 target과 샘플의 거리의 평균을 이용한다. 

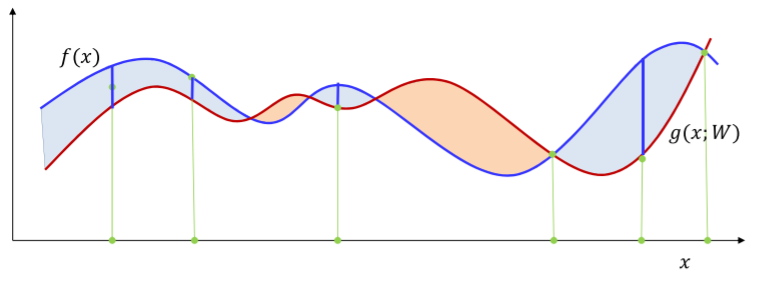
이떄는 모든 부분에서 push up을 해야하고 

이떄는 모든 부분에서 push down해야한다. 이렇게 sample point가 작으면 값의 변동이 커진다. 하지만 sample point를 많이 잡으면

서로 상쇄되어 각각의 sample들의 길이의 의미가 점차 사라지게 된다. variance는 변동과 관련이있음으로 sampel의 수가 작다면 변동성이 커져 variance가 커지고 sample의 수가 많아지면 점차 진짜 loss의 값과 비슷해짐으로 변동성이 작아져 variance가 작아진다. 그렇다면 위는 Batch update일때의 이야기이고 SGD는 샘플포인트 하나만 가지고 계산을 한다. 

따라서 sample이 1개밖에 없음으로 variance가 크다고 할 수 있다. 이것을 수학적으로 나타내면 

loss값은 divergence function의 평균이고 Loss의 평균은 divergence의 평균의 평균이다. 우리는 이것의 최소값을 찾아나가야 한다. 그렇다면 variance는 어떨까

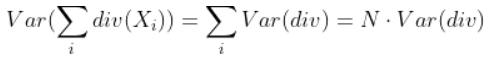
위의 식은 div의 variance이고 Loss의 variance를 위해서는 1/N을 붙여야 한다. 

결론적으로는 sample point의 갯수와 관련 있는 것이고 N이 커질수록 Variance는 작아지게 된다. 아래의 그래프는 SGD와 Batch update를 사용한 결과를 나타내는 그래프이다. 

각각의 막대의 길이가 variance이고 SGD가 variance가 크기 때문에 막대의 길이가 긴 것이다. SGD가 더 빠르게 converge하기는 하지만 에러값은 더 크다. 위 그래프에서 최적의 상태는 시간은 짧고 에러는 줄이는 부분이다(그래프에서 좌하단).

그래서 Mini-Batch update가 등장하였다. Mini-Batch update는 SGD와 Batch update를 섞은 것이다. Random으로 sampel들을 선택하되 그것들을 하나의 batch로 묶어서 update를 한다. 

그에 대한 코드는 아래와 같다. 

위에서 sample의 수가 많을수록 variance가 작아진다고 했는데 이경우는 batch update보다는 아니지만 일정 갯수의 sample들을 가지고 udpate를 진행하기 때문에 variance가 작다. Mini-batch의 경우는 한번 update의 걸리는 시간은이다. SGD가 임으로 Mini-batch가 더 update시간이 적다고 생각할 수도 있는데 SGD보다 b번 더 계산해야 됨으로 더 오래 걸리기는 한다. 하지만 GPU가 나와서 이것의 의미는 무색해졌다. 

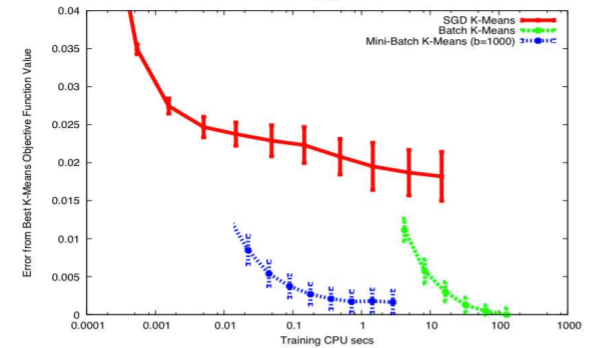
위의 그래프에서 볼 수 있듯이 Mini-Batch가 에러도 적고 시간도 적게 걸리는 것을 확인할 수 있다.