Introduction to Deep Learning Lec2

Multi-layer Perceptrons as Universal Boolean Functions

불리안 게이트는 0,1로 이루어진 게이트이다. 우선 퍼셉트론을 불리안 게이트로 표현해보자.

원안에있는 것이 threshold이다. 이 threshold이상의 수가 들어가야 이 퍼셉트론이 제대로 작동하게 된다. 예른들어 왼쪽 위의 퍼셉트론은 X와 Y가 둘다 1이 들어와야 2이상이 되고 그때서야 작동하게 된다. 이것을 AND Gate라고 한다. 같은 방법으로 오른쪽 위는 NOT Gate, 아래는 OR Gate가 된다. 

위의 Gate를 여러개의 input으로 확장하면 아래와 같이 된다. 

N개의 input이 있고 1~L input이 1이면서 L+1~N이 0일때 L이상이 됨으로 그때서야 작동할 것이다. 이것을 Universal AND Gate라고 한다. 반대로 아래의 그림을 보자

여기서는 1~L중 어떤것들이 1이고 L+1~N중 어떤것이 0이면 무조건 L-N+1의 threshold를 충족시키게 되어있다. 따라서 이것을 Universal OR Gate라고 한다. 

 

하지만 이 방법으로느 XOR Gate를 만들 수는 없다. 단순한 퍼셉트론으로는 만들 수 없고 MLP(Mulit layer perceptron)은 가능하다. 이 퍼셉트론을 여러 층으로 쌓는 것이다. 

이렇게 MLP는 복잡한 boolean function들을 계산할 수 있다. 아래 그림처럼 말이다.

 

따라서 MLP를 Universal Boolean functions라고 한다. 

 

이제 생기는 의문이 얼마나 많은 layer가 필요할지이다. 이를 위해서 한 예를 가져와 보았다. 아래는 어떤 Boolean function의 Truth Table이다.

위의 결과를 MLP으로 나타내면 아래와 같이 표현할 수 있다. 

Y를 product of sum으로 표현하였는데 각각을 하나의 퍼셉트론으로 만들고 그것들을 OR로 묶는 것이다. 모든 Truth table을 얼마나 복잡하든 상관없이 이와 같은 One hidden Layer MLP로 표현 할 수 있다. 

 

아래 카르마 맵을 살펴보자

이것은 카르마 맵으로 만들 수 있는 가장 복잡한 equation이다. 위에서 처럼 표현한 One hidden layer MLP로 표현한다면 각각의 빨간 네모칸을 따로따로 퍼셉트론을 만들어야 하기 때문에 2^(4)/2=2^3의 퍼셉트론이 필요할 것이다. 같은 방식으로 N개의 variable이 있다면 hidden layer에는 2^(N-1)개의 퍼셉트론이 존재하고 exponential하게 증가하게 된다. 이것을 multiple layer로 표현하면 굉장히 쉽게 표현 된다. 우선 위의 카르마맵은 으로 표현이 이 된다. 위에서 XOR를 MLP로 나타낸 방법을 보였는데 같은 방법으로 4 input XOR를 나타내면 아래와 같이 된다. 

One hidden layer에서는 8개가 필요하지만 여기서는 9개의 퍼셉트론이 필요하다. 그렇다면 MLP가 더 표현하기 힘든 것 아이냐 할 수 있는데 input을 늘리면 늘릴수록 MLP의 효과는 더 커지게 된다. 아래는 6 input XOR이다. 

1One hidden layer에서는 2^(6-1)=32개의 퍼셉트론이 필요했지만 여기서는 15개면 충분하다. 각 XOR당 퍼셉트론이 3개씩 필요함으로 N개의 input에서는 3(N-1)개의 퍼셉트론이 필요하게 된다. One hidden layer에서 exponential하게 증가했던것이 Linear하게 증가하는 것으로 바뀌게 되는 것이다. 

파라미터의 수는 네트워크에서 connection의 수인데 이렇게 퍼셉트론이 줄어들면 connection이 줄어들게 됨으로 계산이 더 쉬워지게 된다. 

 

MLPs as Universal Classifiers

하지만 위의 경우들과는 다르게 MLP는 real inputs에서 더 많이 사용된다. 그리고 무언가를 결정하는 decision boundary역할을 하게 된다. 이렇게 real inputs에서 작동하는 perceptron은 real value vector에서 작동하게 되는데 

이렇게 linear classifier로 작동하게 된다(애초에 output y가 weighted sum임으로). 하지만 boolean때와 마찬가지로 XOR에서는 linear classifier로는 분류를 할 수 없게 된다. XOR을 분류하려면 up, down과정이 필요하지만 퍼셉트론으로는 불가능하다. 

이제 Decision Boundary를 직접 만들어 보자. 

위의 오각형은 5개의 선으로 만들 수 있고 각각의 선은 하나의 퍼셉트론을 담당하게 된다. 그리고 이를 AND로 묶으면 오각형의 Decision Boundary를 만들 수 있다. 위와 같은 방법으로 깊게 쌓으면 아래와 같이 오각형 두개도 만들 수 있다. 

이것을 One hidden layer로는 표현할 수 없을까? 그를 위해 아래를 한번 살펴본다.

먼저 Square Decision Boundary를 만들어 보자

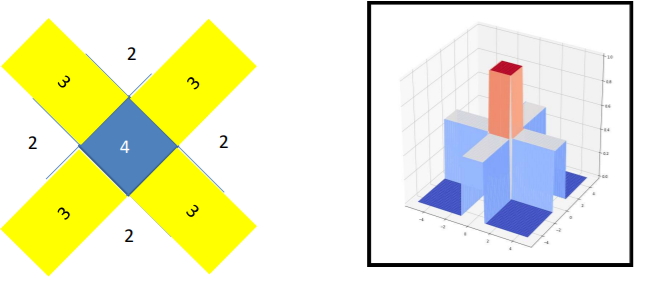
그리고 이것은 아래의 네트워크로 만들 수 있다. 

마찬가지로 오각형, 육각형도 다음과 같이 만들어진다.

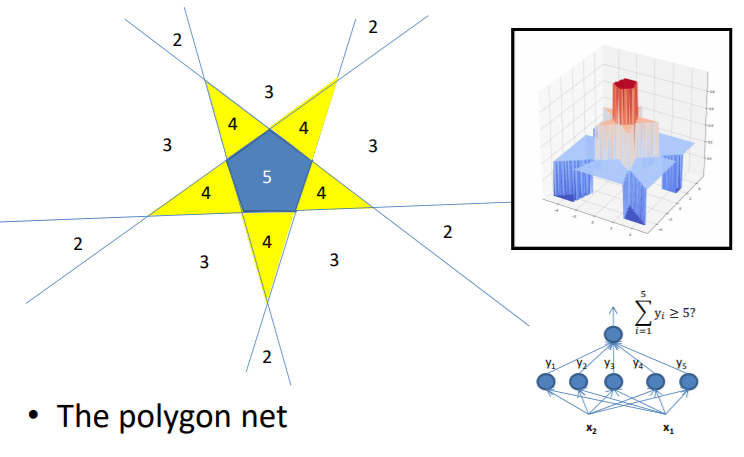
이렇게 계속해서 늘리면 아래와 같은 모양을 얻게 된다. 

이 cylinder의 안쪽은 N이 되고 바깥쪽은 1~N-1임으로 평균으로 N/2를 가지게 된다. 이를 네트워크로 나타내면 아래와 같은데 

계산을 편하게 하기 위하여 실린더 바깥을 0으로 만들기 위해 -N/2라는 bias를 넣어주면 아래와 같이 된다. 

이는 서로 안겹치는 모양이면 같은 평면내에 있으면 위처럼 one hidden layer로 나타낼 수 있음을 나타낸다. 

 

어차피 자기 자신의 실린더 밖은 0으로 계산됨으로 몇개가 오든지 자기 자신 실리더와 겹치지만 않으면 상관없이 그냥 퍼셉트론을 붙이기만 하면 된다. 이를 위의 오각형 두개를 one hidden layer로 나타내는 방법에 적용하면 아래와 같이 된다. 

이렇게 one hidden layer는 모든 classification boundary를 만들 수 있다. 따라서 MLP를 universal classifier라고 한다. 

 

또한 deeper layer와 one hidden layer의 극명한 차이를 볼 수 있다. 아래의 그림을 보면 

deeper layer는 적은 수의 뉴런으로 표현이 가능하지만 one hidden layer는 거의 무한개의 뉴런이 필요하게 된다. 

 

이제 아래의 모양을 네트워크로 나타내어 보자.

이것을 one hidden layer로 나타내면 

위에서 보여준 네트워크와 같이 무한개의 뉴런이 필요하게 된다. 

이것을 two hidden lyaer로 나타내면

 

이고 첫번째 hidden layer는 linear한 64개의 선(대각선으로 각각 8개의 선이 그어진 모양이므로)이 나타내지고 두번째 hidden layer는 첫번째 hidden layer로 만든 linear한 선으로 이루어진 노란색 박스를 찾아냄으로 총 544개의 뉴런이 필요하다. 따라서 총 64+544+1 = 609개의 뉴런이 필요하게 된다. 

하지만 위의 그림은 사실 XOR을 나타낸다. XOR 네트워크로 나타내면 아래와 같이 된다. 

총 253개의 뉴런이 필요하고 12개의 hidden layer로 이루어진다. 

위에서 볼 수 있듯이 deeper and shallower 네트워크는 더 복잡한 패턴을 쉽게 잡아낼 수 있다. 이것을 표현력이 좋다고 말할 수도 있다. 

 

MLP as Universal Approximators

아까는 분류를 했었다면 이번에는 MLP를 이용한 regression을 보일려고 한다. 

아래 그림과 같이 MLP는 continuous한 그래프를 표현 할 수 있다. 

unit(뉴런)들이 많을 수록 더 추상적인 함수를 표현할 수 있다. 하지만 one layer MLP는 single input에 대한 함수만 표현할 수 있다. 하지만 다차원 또한 표현할 수 있는게 위에서 보인 cylinder로 표현할 수 있다. 

One hidden layer네트워크에서 퍼셉트론을 무한개로 늘리면 위와같은 실린더가 나오고 실린더안은 N/2이고 그 밖은 0이다. 각 input당 실린더 하나씩 놓는다면 아래와 같이 여러개의 dimension을 표현할 수 있다. (아래는 2 dimension)

 

이로인해 MLP를 Universal Approximator라고 할 수 있는 것이다. 하지만 주의해야 하는 것이 위에서 output unit이 summation역할을 할때만 해당 된다는 것이다. 

우리가 실제로 사용하는 네트워크는 output이 activation function인 sigmoid, ReLU등으로 이루어져 있다. activation function이 없었다면 아래와 같이 n차원의 output이 나오게 된다.

하지만 이것을 activation function으로 묶으면 정해진 범위의 수로 output을 정할 수 있게 된다. 

Optimal Depth and Width

위에서 보였다시피 single hidden layer MLP는 universal function approximator이다. 하지만 이는 무한개의 뉴런이 존재했을때의 이야기이고 실제로는 유한개의 뉴런이 존재할 뿐이다. 그리고 이 뉴런의 갯수는 표현력에 있어 굉장히 중요하다. 

위의 체크박스 문제를 다시 생각해보자. 

 

이 체크 박스는 각 대각선으로 8개의 선이 존재하고 따라서 위를 2 layer network로 나타내면 첫번째 hidden layer는 선의 갯수인 16개의 뉴런이 존재해야 한다. 하지만 이를 8개로 줄이면 어떤일이 일어날까? 충분히 선을 긋지 못하기 때문에 만일 8개의 뉴런이 존재한다면

이런식으로 8개의 선밖에 긋지 못하게 된다. 그리고 이 체크박스를 완전히 표현하지 못하게 된다. 

하지만 이 적은 갯수의 뉴런에 activation function을 넣는다면 이야기는 달라지게 된다. activation function은 output을 특정한 범위로 표현되게 한다. 그리고 이 것은 곧 자신이 어디에 있는지를 말해주게 된다. 아래그림은 4개의 뉴런으로 첫번째 hidden layer를 표현하고 각 뉴런에 activaton function을 넣었을 때의 그림이다. 

이 시그모이드 함수가 -1~1로 output을 형성하면서 자기의 위치를 다음 layer에게 전달하는 역할을 하게 된다. 만일 activation function이 없었다면 그냥 선만 긋는 셈이 되는 것이고 이는 다음 단에 그어진 선만 전달할뿐 아무 정보도 전달할 수 없다. 

따라서 activation function으로 인해 boundary가 생기고 적은 뉴런으로도 다음 layer에 자기의 위치를 알릴 수 있게 된다. 그리고 여러개의 layer를 겹치면서 저 체크 박스를 형성할 수 있게 된다. 이를 다르게 이야기하면 next layer가 그 전의 layer의 정보를 받아 recover한다고 할 수 있다. 

이렇게 적은 뉴런으로도 네트워크를 구성할 수 있지만 당연히 더 깊은 네트워크가 필요하게 된다. 

 

 

 

 

 

출처 : www.youtube.com/watch?v=-zSSU-aZvIk&list=PLp-0K3kfddPzCnS4CqKphh-zT3aDwybDe&index=9