그래프 : 탐색, 최소 신장 트리
1. 너비 우선 탐색(BFS)
우선 루트의 자식들을 차례로 방문하고, 다음 루트 자식의 자식들을 방문하는 이 과정을 계속 반복하면 된다.
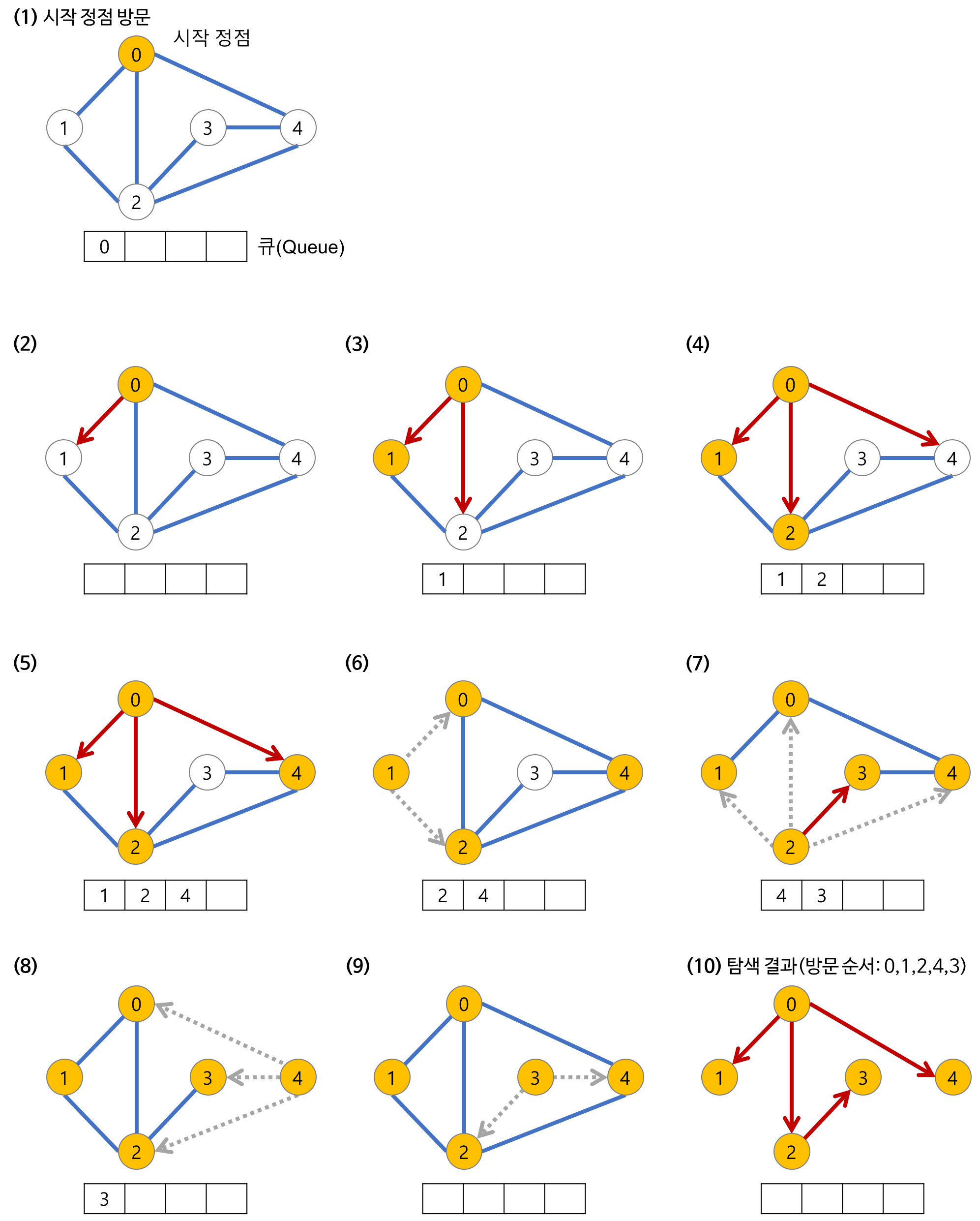
1)먼저 시작 정점을 제외한 모든 정점을 방문하지 않음으로 표시하고 큐에 시작 정점을 넣는다.
2)그뒤 그 큐에 들어있는 정점을 deque해서 인접한 정점을 모두 큐에 넣는다.
3)큐에 들어간 정점들을 방문함 표시를 한다.
4)큐가 빌때까지 반복한다.
마지막 (10)을 보면 트리의 모양을 만들 수 있는데 이를 너비 우선 트리라고 한다.
이를 알고리즘으로 나타내면 아래와 같다.

BFS의 특징은
1) 재귀적으로 동작하지 않는다.
2) 큐를 사용한다.
3) 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 사용한다.
시간 복잡도는 큐에는 V개의 정점이 한번씩 들어갔다 나오고 큐에서 정점을 꺼낼때마다 그 큐에 인접한 간선 E번을 돌게 되어있음으로 Θ(V+E)이다.
2. 깊이 우선 탐색(DFS)

(1) 시작 정점을 선택하고 그것에 인접한 정점으로 이동한다.
(2) 방문한 정점에서 방문하지 않은 다른 인접한 정점으로 이동한다.
(3) 방문한 정점의 인접한 정점이 모두 방문이 되었다면 backtracking으로 돌아간다.
(4) 위를 계속 반복한다.
이과정으로 만들어진 (9)와 같은 트리를 깊이 우선 트리라고 한다.
이를 알고리즘으로 나타내면 아래와 같다.

DFS의 특징은 순환 알고리즘의 형태를 가진다라는 것이다.
시간복잡도는 역시 모든 정점과 간선을 다 돎으로 Θ(V+E)로 나타낼 수 있다.
3. 최소 신장 트리
간선들이 가중치를 갖는 그래프에서 간선 가중치의 합이 가장 작은 트리를 최소 신장 트리(Minimum Spanning Tree)라고 한다.
1) 프림 알고리즘
프림 알고리즘은 집합 S를 공집합에서 시작하여 모든 정점을 포함할 때까지(S=V) 키워나간다. 정점을 하나 더할때마다 간선이 하나씩 확정되는 구조이다. 알고리즘은 아래와 같다.
Primg(G,r)
#G = (V,E) :주어진 그래프
#r : 시작 정점
{
s <= Φ #s는 공집합
for each u ∈ V
d[u] <= ∞;
d[r] <= 0;
while(S≠V){
u <= extractMin(V-S,d);
S <= S∪{u};
for each v ∈ L(u)
if (v∈V-S and w(u,v) < d[v]) then{
d[v] <= w(u,v);
tree[v] <= u;
}
}
}
배열 d[]는 각 정점을 신장 트리에 포함시키는 데 드는 최소 비용을 구하는 것이다. 위에서부터 차례대로 설명하면
1) S집합을 모두 공집합으로 만든다.
2) d 배열을 모두 무한대의 값을 가지게 한다.
3) d 배열의 시작하는 정점 r d[r] = 0으로 둔다
4) S가 다 찰때까지 S를 제외한 집합 V-S에서 최소의 비용을 가지는 정점을 구한다.(u) -> S에 그 정점을 추가한다
5) 4)에서 구한 정점 u의 인접한 정점들을 L(u)라고 하고 그 중 하나를 v라고 하면 v가 S에 들어가지 않고 u,v의 가중치인 w(u,v)가 d[v]보다 작으면 그 값을 d[v]로 하고 tree에 저장한다.
과정은 다음 그림으로 나타낼 수 있다.


(d)의 경우가 5)의 경우이다. 9를 가진 정점의 인접한 정점 중 오른쪽 위에 정점이 원래는 10의 값을 가졌으나 9를 가진 정점과는 가중치가 5로 더 작아서 그 값으로 업데이트 된 경우이다. 이와 같은 것을 이완(Relaxation)이라고 한다.
시간 복잡도는 아래의 이유로 O(ElogV)로 나타낼 수 있다.

2) 크루스칼 알고리즘
크루스칼 알고리즘은 사이클을 만들지 않는 범위에서 최소 비용 간선을 하나씩 더해가면서 최소 신장 트리를 만든다. n개의 정점으로 트리를 만들때 n-1개의 간선이 필요함으로 공집합에서 시작해서 n-1개의 간선이 만들어질때까지 계속 반복한다. 알고리즘은 아래와 같다.

이것의 작동은 아래와 같다.

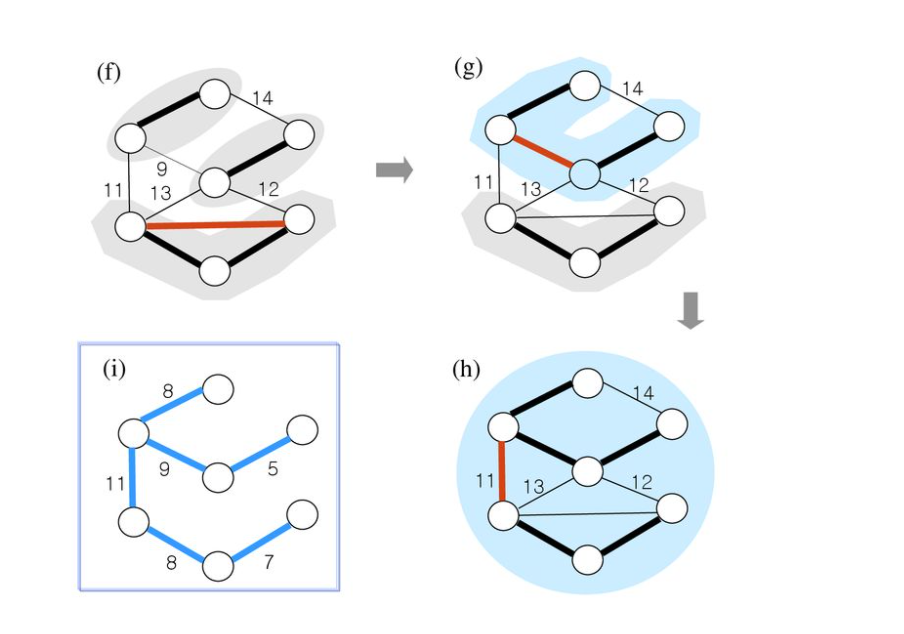
여기서 (f)부분을 조심해야하는데 크루스칼 알고리즘은 사이클을 만들지 않는 범위 내에서 이루어진다. 비록 빨간색 부분의 간선의 값이 8이여서 최소이긴 하지만 양 끝점이 같은 집합에 속하게 됨으로 사이클이 만들어진다. 따라서 이 경우 간선을 버리고 다음 최소 간선을 찾는다.
아래는 시간복잡도계산이다.
1) 3번 정렬에서 O(ElogE) = O(ElogV)를 사용한다.
2) 4번에서 while문은 V-1~E회 반복된다.
3) while에서 최소빈용 간선 제거는 정렬된 배열의 앞부분만 없에면 됨으로 상수시간이 든다.
4) 집합합치는 것은 아래의 정리를 이용한다.

V번의 Make-Set이 필요하고 O(E)번의 find-set과 Union을 수행하므로 위의 정리에 의하여 모두 합친 시간은 O((V+E)log*V)이다. 하지만 log*V는 상수와 다름없다. 그러므로 상수시간이 걸리게 된다.
따라서 총 시간복잡도는 1)에서 걸린 O(ElogV)라고 할 수 있다.