B-트리

1. 특징

B-트리는 다른 이진 트리나 레드 블랙 트리와 달리 한 노드안에 여러개의 키값을 가진다. 이를 다진 검색 트리라고 한다.

위에 처럼 각각의 키값 사이에는 서브트리의 주소가 들어가게 된다. 

B-트리는 다음 2가지의 성질을 만족하게 된다.

1) 루트를 제외한 모든 노드는 |k/2|~k개의 키를 가진다.

2) 모든 리프노드는 같은 깊이를 가진다. 

즉 각 노드는 루트를 제외하면 채울 수 있는 최대 허용량의 반 이상의 키를 채워야하는 것이다. 

 

2. B-트리에서 검색

B-트리에서의 검색은 이진 검색 트리와 같지만 차이점은 한 노드에 여러개의 키가 있다는 것이다. 그래서 찾고자하는 key값이 x라면 key_i-1< x < key_i 를 만족하는 두개의 키값을 찾은 뒤에 그에 해당하는 자식 노드로 내려가야 한다. 이를 재귀적으로 행하면 된다. 

 

3. B-트리에서 삽입

순서는 아래와 같다. 

1) x를 삽입할 리프노드 r을 찾는다.

2) 노드 r에 여유가 있으면 키를 삽입하고 끝낸다. 

3) 노드 r에 여유가 없으면 형제노드를 살핀다. 형제 노드에 여유가 있으면 키를 하나 넘긴다.

4) 형제 노드에 여유가 없으면 가운데 키를 부모 노드에 넘기고 노드를 두개로 나눈다. 만약 부모 노드에 overflow가 발생하면 부모노드를 중심으로 다시 삽입 함수를 실행한다. 

 

예시는 아래와 같다. 

다음과 같은 트리에서 9, 31을 삽입하면 2번째와 4번째 자식노드에 들어가게 되는데 여유가 있음으로 맞는 위치에 넣으면 된다. 

여기에 5를 삽입하려한다. 그러면 첫번째 노드에 들어가게 되는데 5개를 초과함으로 overflow가 발생한다. 그러면 형제 노드를 본다. 형제 노드인 두번째 노드가 여유가 있음으로 overflow된 첫번째 노드의 마지막 원소 6을 부모 노드로 보내고 부모노드의 7을 형제 노드로 보내서 트리의 조건을 맞춘다.

여기에 39를 삽입해본다. 5번째 노드에 들어가게 되는데 마찬가지로 5개를 초과해서 overflow가 발생하게 된다. 이때 형제노드 또한 여유가 없음으로 가운데 값인 40을 부모로 보내고 두개의 노드로 쪼개야 한다.

여기에 23, 35, 36을 넣으면 3, 5번째 자식 노드는 여유가 있음으로 다른 추가적인 행동을 안해도 된다. 

마지막으로 32를 넣어본다. 4번째 자식 노드로 들어가는데 overflow가 발생하고 양쪽 형제 노드또한 여유가 없다. 그러므로 가운데 값인 31을 부모로 보내고 두개로 나눈다.

하지만 부모가 이제 overflow가 발생한다. 따라서 부모를 중심으로 다시 위의 과정을 진행한다. 형제 노드가 없음으로 가운데 노드를 더 위로 보내고(여기서는 루트 노드가 된다), 나머지를 두개의 노드로 나눈다.

 

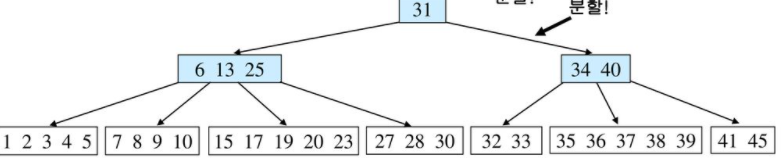
4. B-트리에서 삭제

x값을 삭제한다고 하면 순서는 아래와 같다. 

1) x를 키로 가지고 있는 노드를 찾는다. 

2) 이 노드가 리프 노드가 아니면 x의 직후 원소 y를 가진 리프 노드 r을 찾아 x와 y를 바꾼다. 

3) 리프 노드에서 x를 제거한다. 

4) x 제거후 노드에서 underflow가 발생하면 적절하게 해소한다. 

기본적으로는 이진 검색 트리의 삭제와 비슷한다. underflow는 각각의 노드가 maximum/2보다 많이 키를 가져야 하는데 그렇지 않은 경우이다. 이때는 형제 노드가 여유가 있다면 값을 가져와서 해결하고 그렇지 않다면 형제 노드와 합친다. 합치게 되면 부모 노드의 키값이 하나 필요없게 되는데 이것 역시 합치는 노드에 넣는다. 

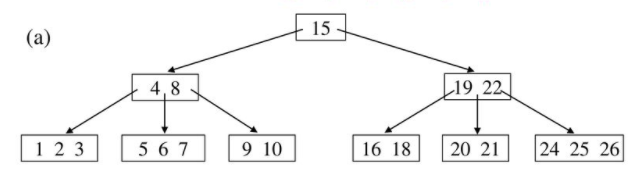
다음과 같은 트리가 있다할때 여기서 7을 삭제하려한다. 어차피 삭제해도 원소는 2개로 maximum의 절반이여서 그냥 진행해도 된다.

여기서 4를 삭제하려한다. 우선 4 다음 크기의 원소를 찾는다. 여기서는 5이다. 그러면 4와 5를 교환한다.

그다음 리프노드에 있는 4를 삭제한다. 이때 그러면 그 노드는 6 한개만 남아서 underflow가 발생하게 된다. 그러면 우선 형제 노드에서 값을 가져 올 수 있는지를 확인한다. 이 경우는 왼쪽 형제에서 3을 가져오면 모든 조건을 만족할 수 있다.

여기서 9를 삭제해본다. 우선 9가 리프이기때문에 그냥 삭제를 한다. 그러면 10 한개만 남는데 underflow가 발생하게 된다.

형제 노드도 가져오면 그 형제 노드가 underflow이기 때문에 가져올 수 없다. 그래서 이번에는 병합을 통해 해결한다. 2번째와 3번째 노드를 합치는데 합친다면 부모노드의 키값이 하나 필요없게 된다. 따라서 부모 노드의 8도 합치는 노드에 넣는다.

그러면 이번에 부모노드가 3 한개로 under flow가 발생한다. 따라서 위의 과정을 다시 진행하여 아래의 트리를 만들면서 종료한다.

 

 

위의 그림은 쉽게배우는 알고리즘 ppt에서 가져왔습니다.