2021. 1. 1. 22:58ㆍ딥러닝 강의 정리
Is BackProp always right?
전의 강의에서는 Back Propagation을 이용한 학습을 보였다. 하지만 이 bakc propagation은 항상 옳을까? 아래의 그림을 보자.

예전 강의에서 Perceptrone으로 linear function을 업데이트하는 과정을 보였다. 이 점들은 Perceptrone 방법이든 Backprop이든 둘다 linear한 function으로 분류가 가능할 것이다. 그렇다면 여기에 하나의 점 "spoiler"를 추가하면 어떻게 될까

Perceptrone방법은 각각의 점에 대응하여 반응함으로 완벽하게 구분짓는 linear한 function으로 수정될 것이다. 하지만 Backprop은 다르다.

빨간색 선이 Backprop 후의 결과이다. Backprop은 미분을 바탕으로 진행 된다. 하지만 여기에는 수천개의 점들이 존재하고 단 하나의 점은 결과에 그리 큰 영향을 끼치지 못한다. 따라서 함수가 완벽히 수정되지 않게 된다.
따라서 Perceptrone방식은 에러가 발생하지 않아 low bias를 가지지만 입력이 하나만 바뀌어도 결과가 크게 바뀜으로 high variance를 가지게 된다. 하지만 Backprop은 차이(div)를 이용하고 수만개중 하나가 추가된것은 그리 큰 차이는 아님으로 low variance를 가지게 된다. 그리고 ML에서는 이 low variance를 선호함으로 Backprop이 이용되는 것이다.
The Loss Surface
학습과정에서 최종적인 목표는 Loss function의 global optimum을 찾는 것이다. 하지만 실제 경우에서 완벽한 global optimum을 찾는 것은 쉬운 일이 아니다. local minima를 찾는 경우도 있고(하지만 이 경우 대부분은 근처에 global optimum이 있다), saddle point를 만나면 stuck해버리는 경우도 있다. 어떠한 경우든 어딘가에 가서 수렴을 하면 converge라고 한다.

Converge를 설명할때는 주로 Convex Loss Function을 이용한다. Convex는 그릇모양의 함수를 이야기 한다. 하지만 주의해야할 것이 이는 어디까지나 설명이 목적이고 실제로는 convex하지 않은 경우가 더 많다.

그리고 업데이트 하는 과정을 3가지 경우로 나눌 수 있다. optimal한 곳으로 정착을 하면 converge이고 왔다갔다 local minimum 근처를 반복하면 jittering, 완벽하게 벗어나버리는 경우를 diverging이라고 한다.
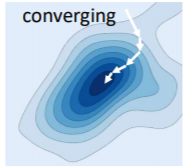


그리고 Convergence rate는 얼마나 빠르게 정답에 도달하느냐를 계산하는 척도이다.

만약 R이 상수라면 convergence가 linear하다고 할 수 있는데 보통은 exponential 하다. .
Convergence for quadratic surfaces
E를 error function이라고 하면 quadratic surface는 아래와 같은 식을 가지게 된다.

E를 한번 미분하면 aw이고 두번 미분하면 a가 된다. a가 만약 양수면 minimum한곳이고, 음수면 maximum한 곳을 가르킨다(E'=0일떄). 여기서 1/2를 곱한 이유는 단지 미분 값이 계산하기 쉽게 나오게 하도록하려고 이다.
또한 w가 update되는 과정은 아래와 같다.

여기서 η는 step size이며 얼마나 빠르게 정답에 도달하는지를 알려주는 parameter이다. 또한 optimal step size는 시작점에서 한번에 정답으로 가는 step size를 이야기 한다. 이를 위해서 E를 tailor series로 나타내본다. Tailor series는 함수를 아래와 같이 나타내는 방법이다.

어차피 w(위에서는 x)는 작을 것이기 떄문에 3번째 항까지만 사용하고 미분을 해보면 아래와 같다.
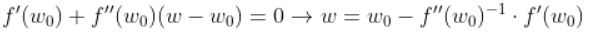
위에서 구한 w의 값을 사용하면 한번의 step만에 optimal 값으로 갈 수 있는 것이다. 그리고 위의 식에서 는

위의 식에서 η의 위치에 있음으로 step size를 이야기 하는 것이다. 따라서 optimal step은 아래와 같이 표현 가능하다.

이값만 있으면 어느 위치에서 시작하든 한번에 optimal로 갈 수 있는 것이다.
그렇다면 optimal step이 아닐 경우는 어떻게 움직이게 될까? 우선 optimal step size보다 작으면 점진적으로 optimal에 다가갈 것이다.

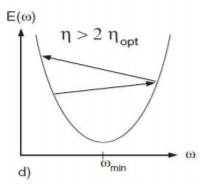
optimal step size보다 크고 optimal step size의 2배보다는 작다면 oscillating하며 결국은 converge하게 될것이다.

만약 optimal step size의 2배보다 크다면 diverge하게 될것이다.
For Functions of Multivariate Inputs
이제 위의 경우를 multivariable에서 다시 생각해보자. 우선 error function은 아래와 같이 정의가 가능하다.

이 function이 quadratic convex function이라면 아래와 같은 형태를 띄게 된다.

그 이유는 아래와 같다.

따라서 E는 결국 N개의 variable이 있으면 N개의 independent한 quadratic function들인 것이다. 그리고 각각의 function에서 맨 앞의 ai는 당연히 양수여야한다.(아래로 볼록이여야 하니깐). 이것의 한 예를 아래 그림으로 보이면

이렇게 각각의 slice가 quadratic function인 것을 볼 수 있다. 그리고 위의 quadratic function일때 optimal step size에서 보았듯이 각각의 경우의 optimal step function은 이다.

그리고 위에서 볼 수 있듯이 각각의 optimal step size는 independent하다.
Vector Update Rule
grdient descent로 update를 할떄는 error function을 w로 미분한 gradient의 반대 방향으로 update를 하면 된다. 따라서 이것의 의미는 error function의 contour의 수직인 방향으로 계속 나아가다보면 언젠가는 optimal한 중심으로 가게 된다는 것이다.
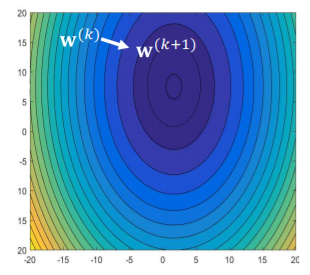
그리고 learning rate는 모든 w에 동일하게 적용되어야 한다. 하지만 여기서 문제가 발생하는데 위에서 optimal step size의 2배 보다 learning rate가 커진다면 diverge하게 된다고 하였다. 그렇다면 모든 w에 적용되는 learning rate는 어떤 것을 선택해야 할까? 이를 방지하기 위해 만들 수 있는 optimal step size 중 가장 작은 것의 2배보다 작게 한다.
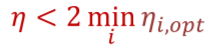
이 방법은 언제가는 수렴이 되겠지만 어떤 component한테는 oscilate converge의 조건으로 되어서 매우 느리게 converge하게 된다.

첫번째 그림은 learning rate가 n2의 2배이고 n1의 optimal step size보다는 작기 때문에 w1(수직방향)으로는 converge하지만 w2(수평방향)으로는 diverge하게 된다.
두번째 그림은 learning rate가 n2의 딱 2배이면서 n1의 optimal step size보다는 작기 때문에 w1에서는 monotically converge하고 w2에서는 oscillating converge하게 된다.
4번째 그림은 learning rate가 n1이랑 같음으로 w1방향으로는 한번의 step으로 optimal 영역을 찾고 w2는 monotically converge하는 것을 볼 수 있다.
하지만 위의 경우는 variable이 몇개 없어서 그림으로 쉽게 알 수 있는 거지 실제로는 전혀 예측이 불가능 하다. 그래서 비율을 주로 사용한다. 빠르게 converge하려면 ideally하게는 learning rate가 가장 큰 learning rate와 가장 작은 learning rate 둘다와 가까운 값이여야 한다. 하지만 이것은 불가능하다. 그래서 만약 이 크다면 converge하는 속도가 느린 것으로 판단한다.
하지만 위의 방법의 문제는 loss function의 이심률이 모든 방향에서 같지 않고(방향이란 각 w의 방향으로 slice해서 나온 결과를 이야기한다) 달라져서 각 component마다 learning rate가 달라 어떤 것을 선택하기가 쉽지 않다.

그래서 이 문제를 해결하기 위해 각 축을 scaling하는 것이다. 그 다음 원으로 만든다면 모든 방향에서 learning rate가 같아지는 효과를 볼 수 있을 것이다.

위에처럼 scailing을 하게 되면 그 결과의 error function은 아래와 같이 바뀌게 된다. A가 원래는 각 component들의 볼록한 정도를 나타내는데 원으로 scailing을 해버리니 A가 indentity matrix가 되어 사라지게 된다. 그리고 이때의 optimal step size는 당연히 1이 되게 된다.

그렇다면 scaling factor인 S는 어떻게 정하면 될까.

파란색과 빨간색 식이 같아야 함으로

따라서
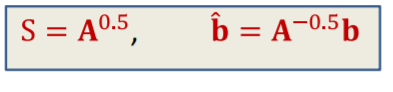
위에가 scaling factor가 된다.
이제 위에서 scaling한 결과를 이용하여 gradient descent를 진행해보자. 먼저 gradient를 구해야 하는데 그 결과는 아래와 같다.

따라서 위에서 구한 gradient를 update 식에 대입하면

가 나오게 된다.
이제 위의 방법을 multivariate convex function에 대입해보자. 우선 error function을 tailor series로 변환하면 아래의 식으로 된다.

이 식은 quadratic form인 를 가지고 있는데 바로 2번째 항이다 그리고 이때의 A부분은 hessian matrix가 담당한다. 따라서 위에서 했던 update식에서 A부분을 hessian으로 바꾸면 된다.

그리고 이때 역시 optimal step size가 1임으로 learning rate를 1로 두면 한번에 optimal로 가게 된다. 그 방법은 아래와 같다.





각각의 경우에 위의 방법을 적용하면 optimal한 곳으로 converge하는 것을 볼 수 있다.
이방법은 하지만 문제가 있다. 우선 Hessian matrix를 계산하는 것은 매우 시간이 오래걸린다. 그리고 hessian이 positive여야 아래로 볼록한 convex function을 의미하는데 non convex function에서는 hessian이 음수일 경우도 있고 이때는 diverge하게 된다.
또한 learning rate에 대한 문제도 존재하는데 앞에서 optimal step size의 2배보다 작아야지 converge하게 된다고 하였다. 하지만 실제로는 converge하는 장소가 문제가 된다. 정답을 위해서는 global minimum에 converge해야 하는데 실제 function은 단순히 convex하게 생기지 않고 local minimum도 같이 존재하게 된다. 따라서 converge하는 위치가 local minimum이여서 더 loss값을 줄일 수 있는데 못하는 경우가 생긴다. 이때는 오히려 learning rate를 optimal step size의 두배보다 크게해서 그 영역을 탈출시켜 해결 할 수 있다.
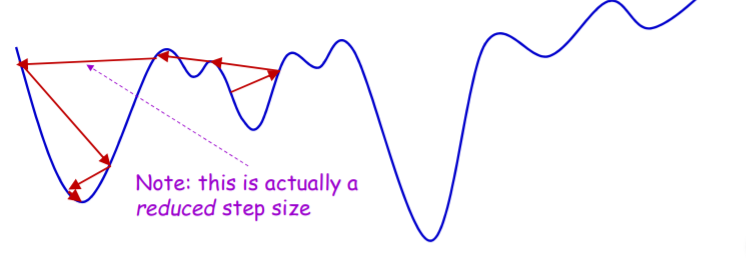
따라서 시작할때 learning rate를 2보다 크게 하고(이경우는 위에 normalize를 한뒤로 생각한다) 그다음 점차 learning rate를 줄여가면 효과적으로 optimal을 찾을 수 있다. 일반적으로는 fixed learning rate를 가지고 loss값의 변화가 없을 때까지 사용한 뒤 loss의 변화가 미비하면 그때 learning rate를 줄여나가는 방법을 많이 사용한다. 그리고 줄여가는 정도는 아래중 하나를 선택하면 된다.

Inspired Algorithm : RProp, QuickProp
위의 경우에 생기는 문제점들은 모두 learning rate를 모든 component에게 일괄적으로 적용해서 생긴 것이다. 각각의 comonent들이 따로 움직이는 방법은 없을까? RProp이 바로 그 방법이다. 이 방법은 우선 하나의 initial value w를 정한다음 그것의 derivative를 계산한다. 그다음 집중해야할 것은 그 값이 아닌 부호이다. 그 derivative의 부호에 일정한 값을 곱하여 update를 하는 방식이다.


다음 step에서 전 step의 부호와 같다면 step size를 늘려서 더 큰 보폭으로 나아가게 한다.

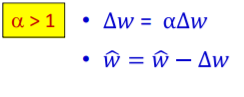

그러다가 부호가 바뀌면 다시 그전의 위치로 돌아간다.


그다음 다시 step을 나아가는데 step size를 줄여서 나아가는 것이다.


정리하자면 계속 앞으로 나아가다 derivative의 부호가 바뀌면 다시 바뀌기 바로 직전 위치로 돌아가 step size를 줄인다음 다음 step을 진행하는 방식이다. 이방법은 단순히 일차 미분만 생각하고 그 이외의 convexity등은 고려하지 않기 때문에 gradient descent보다 어떨때는 더 효과적이기도 하다.
QuickProp은 위에서 Newton update 방식을 수정한 것이다. 우선 Newton update는 아래의 방식으로 이루어진다.


이 식에서 이제 각각의 dimension을 independent하게 다루는 것이다. 위의 식에서는 일괄적으로 Hessian을 이용해 이차 미분을 진행했다면 Qucick prop은 각각의 dimension의 이차미분을 hessian으로 생각하고 진행한다. 그리고 그 이차미분도 approximate하게 진행한다.

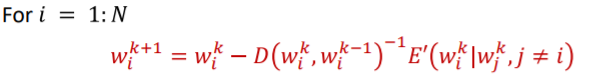
D의 자리가 hessian위치인데 이 D는 직접 계산하는 것이 아닌 각 일차 미분의 차이를 이용한다.

그리고 delta w는 아래와 같다.

이 방법은 non convex objective function에 적합하며 가장빠른 알고리즘중 하나로 분류 된다.
하지만 위의 RProp과 QuickProp은 각각의 dimension을 independent하게 다루기 때문에 결과적으로 우리가 원하는 곳에 도착을 하지 않는 경우가 생길 수 있다. 또한 만일 기울기의 부호가 달라지면 다시 바로 전 step의 위치로 돌아가는데 각가의 dimension이 따로 움직이니 어느 dimensiion에서는 앞으로 나아가고 어느 dimension은 diverge해서 다시 원래 위치로 돌아가곤 한다. 이경우 전체적으로 바라보았을때 왔다갔다 제자리에 위치할 수 있을 것이다.
'딥러닝 강의 정리' 카테고리의 다른 글
| Training Optimizers and Regularizers/Lec 7. (0) | 2021.01.03 |
|---|---|
| Training Neural Networks: Optimization/ Lec6. (0) | 2021.01.02 |
| Learning the Network : BackProp/Lec 4 (0) | 2021.01.01 |
| Learning the network: Part 1/Lec3 (0) | 2021.01.01 |
| Introduction to Deep Learning Lec2 (0) | 2021.01.01 |