2021. 2. 5. 17:54ㆍ알고리즘
1. 병합 정렬(merge sort)
이 알고리즘은 입력을 반으로 나누고 나눈 앞부분과 뒷부분을 따로 정렬을 한다. 그다음에 그 정렬된 배열을 다시 합치는 방식이다. 알고리즘은 아래와 같다.

아래는 구현 과정이다.

merge부분은 비교적 간단한데 정렬된 A[p...q], A[q+1...r]을 하나씩 비교하며 작은 것을 새로운 배열인 temp에 넣고 나중에 temp에 들어있는 내용을 A 배열로 다시 옮기면 된다. 직접 구현한 코드는 아래와 같다.
def mergesort(A, p, r):
if p<r:
q = (p+r)//2
mergesort(A, p, q)
mergesort(A, q+1, r)
merge(A, p, q, r)
return A
def merge(A, p, q, r):
temp = []
i = 0
j = 0
t = 0
while (p+i<=q) and (q+1+j<=r):
if A[p+i]<A[q+1+j]:
temp.append(A[p+i])
i += 1
t += 1
else:
temp.append(A[q+1+j])
j += 1
t += 1
#sort if left list is not sorted
while p+i<=q:
temp.append(A[p+i])
i += 1
t += 1
#sort if right list is not sorted
while q+1+j<=r:
temp.append(A[q+1+j])
j += 1
t += 1
#store the temp list into orginal list
t = 0
while p+t<=r:
A[p+t] = temp[t]
t += 1
return A
이 시간복잡도는 아래와 같이 계산된다.

여기서 인 이유는 어떤 정수 n과 2n 사이에는 항상
가 존재하고
일때 시간복잡도를 보면
임으로
으로 두어도 시간복잡도 계산에서 문제점이 생기지 않는다.
2. 퀵 정렬(Quick Sort)
퀵 정렬은 평균적으로 가장 좋은 성능을 가져 자주 사용되는 정렬이다. 알고리즘은 아래와 같다.

배열에서 기준원소를 고른뒤 (여기서는 맨 마지막 원소를 기준으로 두었다) 이 기준원소를 중심으로 기준 원소보다 작으면 왼쪽, 크면 오른쪽으로 구역을 나눈다. 이것이 partition에서 하는 일이다. 그리고 partition함수에서 기준원소가 최종적으로 자리하게 되는 위치를 return하면 그 위치의 양쪽을 다시 quicksort하면 된다.
병합정렬이 재귀적으로 작은 문제를 해결한다음 후처리를 하는데에 비해 퀵 정렬은 먼저 선행으로 정렬을 시켜놓은다음에 재귀적으로 작은 문제를 해결하면서 바로 끝내게 된다. 아래는 퀵정렬의 예시이다.

직접 구현한 코드는 아래와 같다.
def quickSort(A, p, r):
if p < r:
q = partition(A, p, r)
quickSort(A, p, q-1)
quickSort(A, q+1, r)
return A
def partition(A, p, r):
#choose last element of selected list as a standard element x
#three parts
#parts 1 : i -> less than standard element x
#part 2 -> larger than standard element x
#part 3 : j -> not selected yet
x = A[r]
#make part 1
i = p
#make part 2, j stands for part 3 that are not selected yet
for j in range(p, r):
#if A[j] is less than standard element make a room for part 1
#and swap with part 3
if A[j] <= x:
temp = A[i]
A[i] = A[j]
A[j] = temp
i += 1
#move standard element between part 1 and part 2
#we already make a room in last for statement so we don't have to
#i+1 at this time
temp = A[i]
A[i] = x
A[r] = temp
return i시간복잡도는 두가지 경우가 있는데 우선 가장 이상적인 경우는 partition 이후에 반환된 값을 기준으로 양쪽이 반반으로 나누어졌을때이다. partition은 배열을 한번 다 훑는 것임으로 Θ(n)이고 전체 시간복잡도는 재귀적으로 으로 나타낼 수 있다. 그리고 이 경우는 병합정렬과 마찬가지로
이 된다.
반면 최악의 경우는 partition이후에 나누어지는데 한쪽으로 다 몰려있는 경우이다. 이때의 전체 시간복잡도는 이므로 아래에 의해
이 나온다.
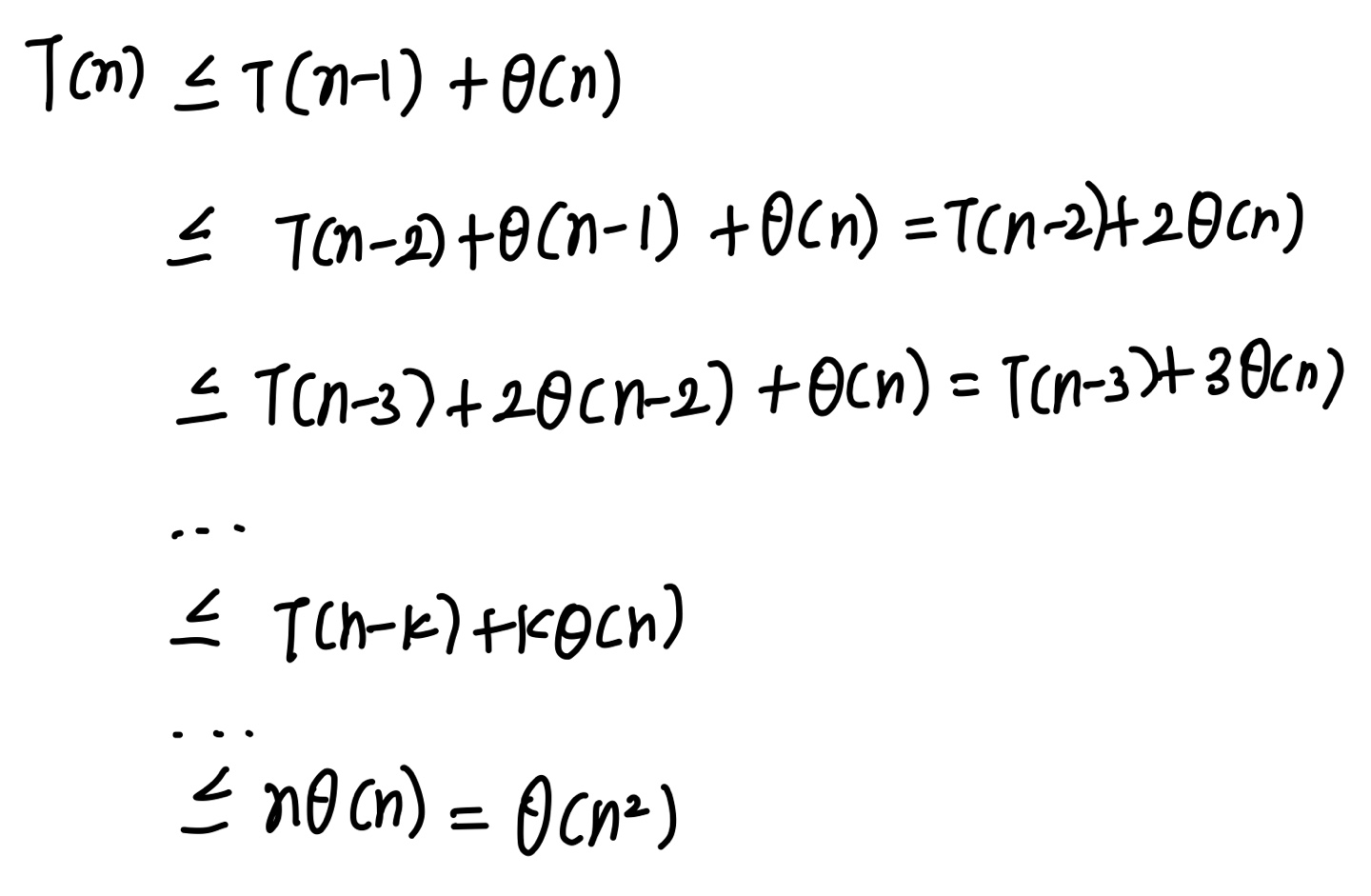
평균적인 경우는 partition이후에 반환된 값이 i라면 왼쪽은 i-1개, 오른쪽은 n-i개의 원소가 있게 됨으로 이고 i는 0~n까지 가능함으로 이값을 평균을 내면
이 나오게 된다. 이 값은 아래에 의해 Θ(nlogn)이 나온다.

3.힙정렬(Heap sort)
우선 힙은 이진트리로서 맨 아래층을 제외하고 모두 채워져 있고 맨 아래는 왼쪽부터 채워나간다. 또한 각 노드의 값은 자기 자신 값보다 작다라는 힙성질을 만족하게 된다.(여기서는 최소힙을 사용해서 이 성질을 만족하게 된다.) 아래는 힙의 모양과 이것을 배열로 표현하는 방법이다.

A[k]의 자식은 A[2k], A[2k+1]이된다. 힙을 만드는 코드를 직접 구현한 결과는 아래와 같다.
def buildHeap(A, n):
#build heap from bottom
for i in range(n//2, 0, -1):
heapify(A, i, n)
def heapify(A, k, n):
left = 2k
right = 2k+1
#check the right node
if right <= n:
if A[left] <= A[right]:
smaller = left
else:
smaller = right
#check the left node if there's no right node
elif left <= n:
smaller = left
#if there's no node, then k is leaf node->end the function
else:
return
#if parent is smaller than left or right node-> swap
if A[k] >= A[smaller]:
temp = A[k]
A[k] = A[smaller]
A[smaller] = tempheapify는 A[k]에 달려있는 두개의 서브 트리가 힙성질을 만족할때 A[k]를 루트로 하는 서브트리가 힙성질을 만족하게 만드는 함수이다. 이미 왼쪽과 오른쪽 서브트리가 힙성질을 만족함으로 그 두개의 서브트리의 루트 즉 A[k]의 노드의 값들을 비교해 A[k]보다 작다면 A[k]와 swap을 하고 swap된 곳을 기준으로 다시 heapify를 하는 형태이다. 그리고 그 서브트리가 만약 없다면 리프임으로 함수를 끝낸다. 또한 buildHeap은 heapify함수가 A[k]아래의 서브트리가 이미 힙성질을 만족함을 가정함으로 아래서부터 위로 올라가는 형태로 만든다.
heapify의 시간복잡도는 트리의 높이와 관련이 있다. 한층에 O(1)씩 걸리고 트리의 높이는 을 넘지 않음으로 시간복잡도는 logn이 나온다. 하지만 이는 모든경우에 적용하기 힘든 것이 맨처음 호출되는 heapify는 리프 바로 위임으로 트리 높이가 1밖에 안되고 그다음 레벨은 높이가 2여서 모든 경우에 이렇게 대입하기 힘들다. 따라서 이 경우들을 모두 더하면 n층일때 nlogn이 아닌 그냥
이 나오게 된다.
이를 이용해서 정렬을 하는 과정은 다음과 같다. 우선 주어진 배열을 buildheap을 이용하여 힙을 만든다. 그다음 맨 위의 노드와 리프노드중 가장 마지막 element를 교환한다. 그다음 heapify를 이용해 힙성질을 만족하게 만든다. 교환을 한다음에는 원래대로라면 새로운 배열의 첫번째에 그 맨 위의 노드의 요소를 넣어야하겠지만 공간 절약을 위해 그냥 현재 배열의 맨 마지막(리프노드의 가장 마지막 element가 있던 자리)에 두고 배열의 크기가 1줄었다고 생각한다. 이를 계속 반복하면 배열이 역순으로 정렬이 될것이며 이를 반대로 돌려주기만 하면 된다.
아래는 직접 구현해본 코드이다.
def heapSort(A, n):
#At first, make a list as a heap
buildHeap(A, len(A))
list_len = len(A)
for i in range(len(A)-1, 0, -1):
#exchange between current element and top node
temp = A[i]
A[i] = A[0]
A[0] = temp
#decrease the list size
list_len -= 1
#compare between changed current element and child nodes
#if current node is greater than child nodes, than heapify
#and make list as a heap again
heapify(A, 0, list_len)
#reverse the list
for i in range(len(A)//2):
temp = A[i]
A[i] = A[(len(A)-1)-i]
A[(len(A)-1)-i] = temp
return A
이때 걸리는 시간복잡도는 buildheap은 Θ(n)이고 heapify는 매번 첫번째 단계에서 리프노드단계까지 heapify가 실행된다고 하면 for문 한번당 Θ(logn)이고 for문을 n번돔으로 Θ(nlogn)이나오게 된다.
'알고리즘' 카테고리의 다른 글
| 선택 알고리즘 (0) | 2021.02.09 |
|---|---|
| 특수 정렬 알고리즘 (0) | 2021.02.07 |
| 기본적인 정렬 알고리즘 (0) | 2021.02.04 |
| 점화식과 알고리즘 복잡도 분석 (0) | 2021.02.02 |
| 점근적 표기 (0) | 2021.02.01 |