2021. 1. 4. 11:28ㆍ카테고리 없음
Scanning
지금까지는 MLP를 이용한 단순한 훈련을 진행하였다. 하지만 아래의 경우는 어떠할까?

위에 목소리에서 Welcome이라는 단어가 들어있는지를 알 수 있을까? 우리가 지금까지 한 방법으로 아래와 같이 training을 시킬 수 있다.
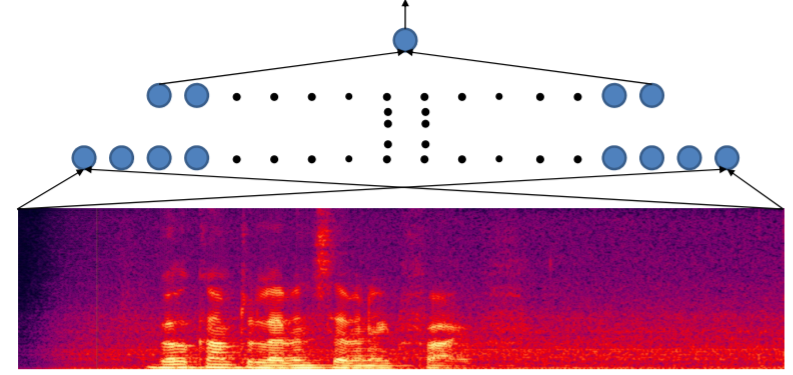
하지만 이방법의 문제점은 MLP가 패턴인식과 같기때문에 어느 한 위치에 Welcome이 있으면 다른 한 위치에 있는 Welcome은 못 찾아낸다는 것이다. 즉

위의 그림에서 첫번째 박스와 두번째 박스의 Welcome을 구별하지 못하는 것이다. 이 둘을 구별하려면 엄청난 양의 데이터를 통해 학습을 해야 한다. 모든 구간에 Welcome의 파형을 알고 있어야 하기 때문이다. 하지만 우리가 원하는 것은 Welcome의 위치가 아닌 그저 Welcome의 유무이다. 이것을 shift invariance라고 한다. 우리가 구현하고자하는 네트워크는 shift invariant여야 한다.
이것을 해결할 방법은 없을까? 그 해결방법중 하나는 scan이다. 아래 그림을 보면




이런식으로 작은 박스의 내용을 MLP에 넣음으로서 구현이 가능하다. 그리고 마지막을 Max로 묶으면 각각의 MLP의 결과들중 1에 가까운 부분이 Welcome이 있는 곳이라는 것이다. 아니면 Max대신 적절한 softmax 또는 MLP를 넣어도 해결이 가능하다. 위 방법의 코드는 아래와 같다.

만일 위에 각각의 MLP가 다 같은 것이라면 위의 과정을 하나의 큰 network로 봐도 된다. 어차피 각각의 박스를 같은 네트워크로 훈련하기 때문이다. 그리고 이것을 shared parameter network라고 한다.
이번에는 이미지를 보자. 이미지도 마찬가지 방법을 이용하면 된다. 차이점이 있다면 위의 소리는 좌우만 scan한다면 이미지는 상하좌우가 있기때문에 상하부분도 체크해야 한다.





각각의 input이 pixel data이고 마찬가지로 마지막을 max나 softmax또는 MLP로 묶으면 된다. 위의 코드는 소리때와 마찬가지인데 상하를 나타내는 j부분이 추가되었다.

그리고 이것역시 각각의 MLP를 같은 것을 사용하면 하나의 큰 네트워크로 생각할 수 있다.
Shared Parameter Networks
Shared parameter network는 위에서 보았듯이 각각의 MLP가 weight를 공유하는 network이다. 이것을 아래처럼 정의할 수 있다.

이것은 를 바꾸는 것이 곳
을 바꾸는 것과 같으며 div로 바꾸는 것이다. 그 관계도는 아래와 같다.

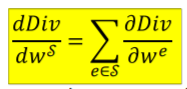
따라서 위의 shared parameter network를 코드로 나타내면 아래와 같아진다.

여기서 파라낵 박스부분인 Loss의 gradient에서 S에는 많은 parametere들이 있어 이것을 펼치면 아래와 같은 모습이 나온다.

각각의 parameter에 대해 gradient를 구한뒤 더하는 것이다.
Another Look of Scanning
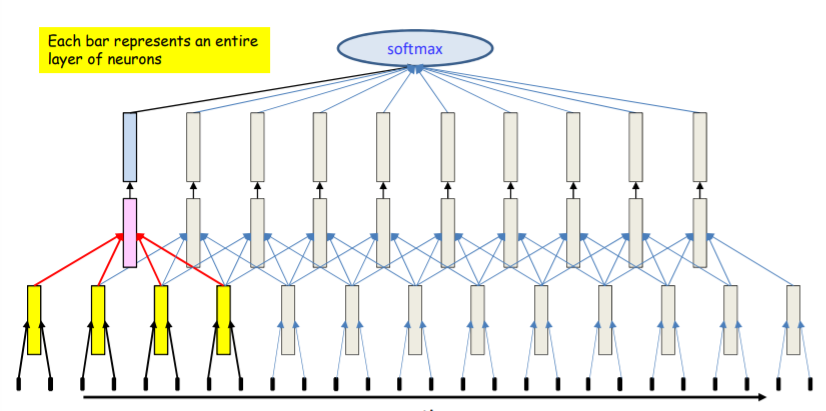
위의 scanning을 다시한번 과정을 나타내면 아래와 같다.
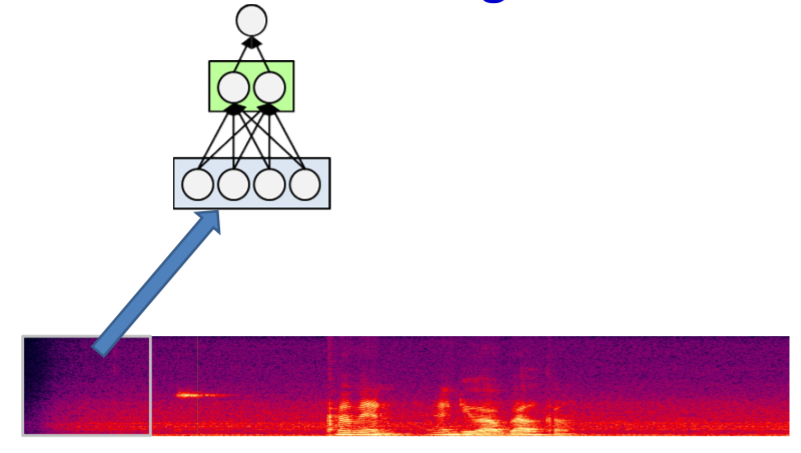



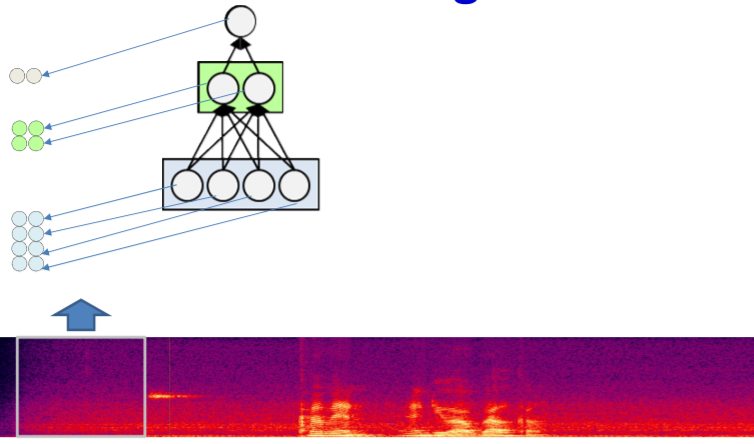
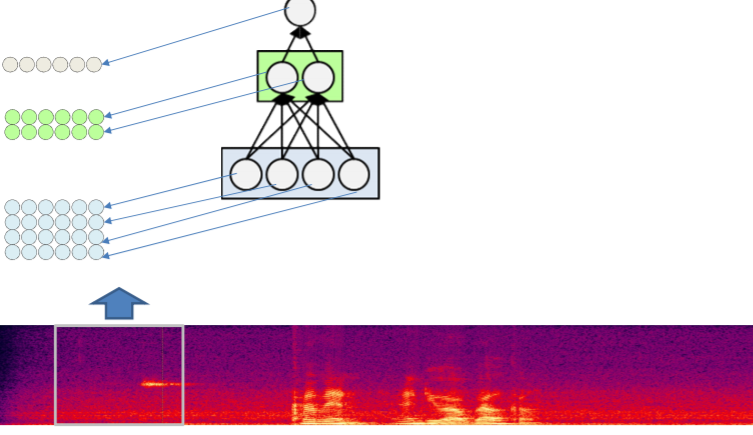

위처럼 각각의 box에 한번에 MLP를 돌리며 나아가는 구조이다. 그렇다면 이번에는 한번에 한 뉴런씩 training을 시켜보자.
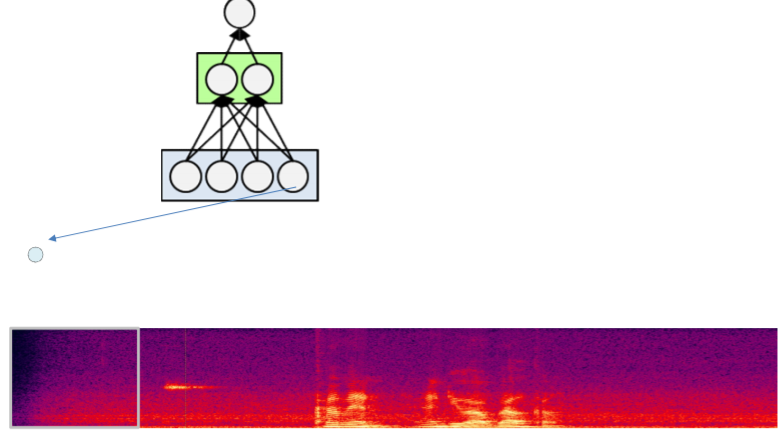
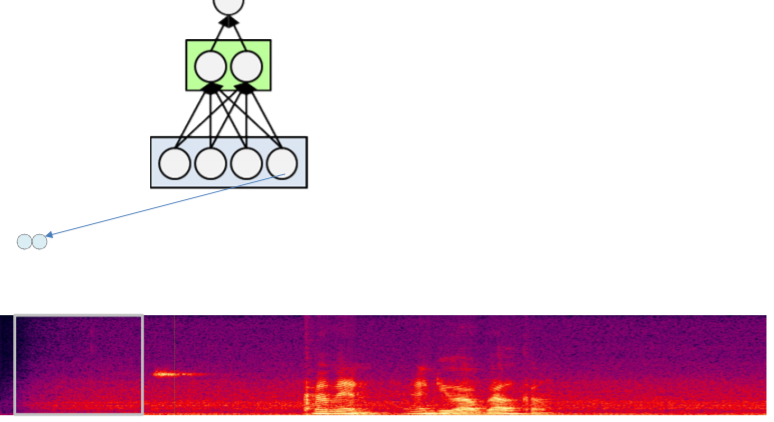




일층의 뉴런들을 다 계산했음으로 이번엔 이층을 계산한다.



이제 마지막층을 계산하고 softmax를 한다.

위의 방식으로 해도 처음에 한 방법과 순서만 달라질뿐 계산에는 전혀 다른 점이 없다. 그 코드는 아래와 같다.

먼저 l이라는 layer를 선택한다. 그다음 각 time t마다 j라는 뉴런을 선택하여 모든 T에 대하여 돌리는 것이다. l==1일때는 input일때는 의미함으로 inputd x를 함수에 넣고 그다음 layer부터는 그 전 layer의 결과를 받아서 넣는다. 이것을 vector notation으로 표현하면 아래와 같다.

이미지를 scanning 할때도 마찬가지 방법으로 한뉴런에 대하여 모든 부분을 먼저 scan하면 아래와 같은 방식으로 진행된다.





그다음 두번째 layer를 같은 위치에서 뽑아내어 진행한다.
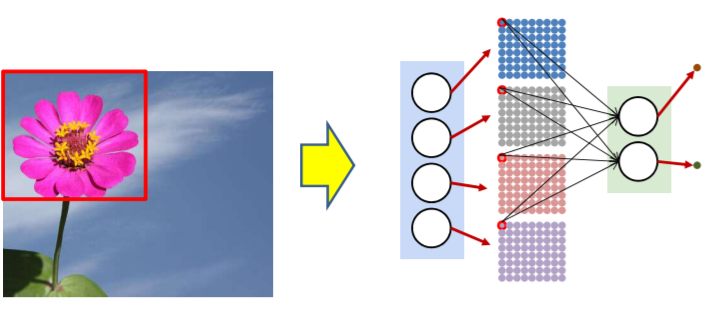


그뒤 마지막 레이어 역시 같은 위치에서 뽑아내어서 진행한다.

마지막 뉴런은 아래 처럼 max를 해서 꽃이 있는 위치를 알거나

flatten을 한뒤에 softmax 또는 적절한 MLP를 넣어 꽃의 위치를 찾으면 된다.

위 과정의 코드는 아래와 같다. W는 width이고 H는 height이다. 그리고 K는 각 박스의 크기이다.

l번쨰 layer를 선택한뒤에 j번째 뉴런을 선택하고 x와 y에 맞는 위치의 값을 계산하면 된다.
이러한 방식으로 진행하면 각 layer는 어떤 것을 배우게 되는 것일까? 그를 위해 예전에 했던 오각형 두개를 파악하는 네트워크를 다시 생각해보자.

위의 네트워크에서 첫번째 layer는 linear한 선을 나타내였고 그 선을 두번째 layer에서 묶어서 각각의 오각형을 만들었다. 그리고 마지막 layer에서 그 두 오각형을 합쳐서 두번째 보다 더 복잡한 도형을 표현하였다. 이렇게 layer는 깊어질 수록 더 복잡한 패턴을 인식하게 된다.
Distributing the Scan
위에서 했던 scanning은 단지 꽃의 유무정도만을 알 수 있다. 이번에는 각각의 위치에 꽃의 pattern이 있는지를 확인해보자. 위에서 했던 scanning을 다시 응용을 해보면된다. window를 설정한뒤 그 window가 하나의 큰 이미지라고 생각하고 진행한다.




이렇게 하면 하나의 박스에 대한 전체의 계산을 마치게된다. 그리고 여기서는 edge정도의 기초적인 정보만을 알아낼 수 있다. 이것이 두번째 layer로 가면 첫번째 block의 전체적인 output이 들어가게 된다.

이렇게 하면 좀더 효율적으로 큰 block에 대한 패턴을 인식할 수 있게 된다. 왜냐하면 이 묶음들이 다음 layer로 간다는 것은 아래 그림처럼 9의 픽셀 data로 이루어진 data가 다음 layer로 간다는 것이기 때문이다.

그리고 마지막 layer는 결국 전체의 그림의 모습을 보는 형상을 띈다(아래 그림은 위의 네트워크와는 조금 다르지만 비슷한 내용이다.).

위의 방식을 Scanning with distribution이라고 한다.
그렇다면 전에 했던 distribution없을 때와는 어떠한 차이점이 있을까? Scanning without distribution때는 각각의 정해진 크기의 pixel data가 결국은 하나의 MLP씩을 통과했기 때문에 아래의 형태를 띈다.

하지만 distribution을 했으면 묶음 다발이 다음 layer로 들어가기 때문에 좀더 간결한 형태를 띈다.
위의 코드를 아래처럼 나타낼 수 있다.

박스 안을 집중해보면 박스안은 우선 바로 전 layer의 input을 i를 통해 가져오고 box의 크기만큼 x'와 y'를 잡는다 그리고 w를 통해 각각의 input과 weight를 component by component로 합쳐서 z에 넣는다. 이방법을 CONVOLUTION이라고 한다.
Why Using Distributed Scanning?
앞에서 distributed scanning을 살펴보았다. 그렇다면 이것이 왜 더 효율적이라는 것일까? 아래는 distribution을 사용하지 않은 scanning이다. (1d이고 소리 문제라고 생각하면 된다)

intput layer에서 사용되는 parameter는 8개의 input이 N1에 들어감으로 8D*N1이다. 1,2 layer에서의 parameter는 N1*N2개이고 그다음단은 N2*N3개 마지막은 N3개의 parameter가 사용된다. 옆으로 계속 scanning해도 어차피 weight는 공유됨으로 상관이 없다.
그렇다면 위를 distribution을 사용하면 어떻게 될까?

마찬가지로 parameter의 갯수를 살펴보면 첫번째는 2개의 input이 다음 layer에 들어간다. 따라서 2D*N1개가 필요하다. 그다음 layer는 4개의 N1이 N2로 들어감으로 4*N1*N2개가 필요하다. 그 다음은 N2가 N3로 그냥 들어감으로 N2*N3개가 필요함으로 총 필요한 parameter의 갯수는 아래와 같다.

하지만 같은 network에서 distribute를 안한다면 8개의 input이 4개의 N1에 각각 들어가게 됨으로 첫번째 layer가 8D(4N1)이 나오게 된다. 따라서 더 많은 parameter가 필요하게 된다.
위의 네트워크를 전부다 돌리면 아래의 형상이 나온다.

여기서 파란색 동그라미 부분이 N2의 2군데에 공유되게 된다. 이렇게 distribution을 사용하면 계산량이 줄어들기도 한다.
Modification of Network
위에서 설명한 네트워크의 과정을 아래로 풀어서 말할 수 있다. 먼저 첫번째 layer는 main image의 매우 작은 영역을 탐색한다. 예를들어 꽃사진에서 꽃잎같은 부분이다.
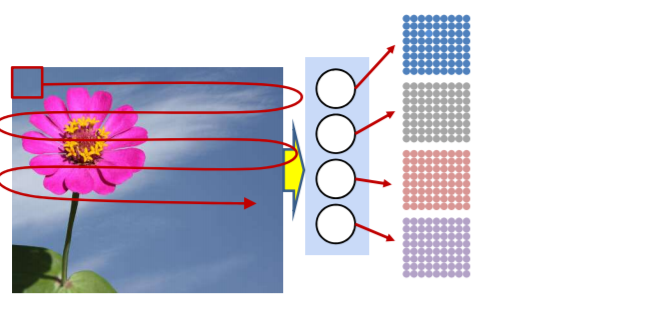
그 다음 영역은 첫번째 layer의 output이 들어간다. 예를들어 꽃을 탐지하기 위해 첫번째 layer에서 찾은 꽃잎들을 붙이는 역할이다. 첫번째 보다 좀더 넓은 영역을 탐지한다.

이런식으로 계속 탐지 영역을 넓혀나가면서 꽃의 패턴을 찾는 것이다.

이때 각각의 scanning neuron을 filter라고 한다. 그리고 높은 단계의 filter일수록 좀 더 명확해지는 모습을 보인다. (사실은 꽃잎등이 명확하게 보이지는 않는다. 단지 예시일 뿐이다)
그리고 마지막 단을 MLP에 넣는다.

이 과정에서 몇가지 수정을 해보자. 우선 filter를 위에서는 한 픽셀씩 움직였는데 꼭 이럴 필요는 없이 몇 픽셀씩 움직여도 된다. 이때 움직이는 범위를 stride라고 한다. 이렇게 해도 결과에는 큰 지장이 없으며 계산을 줄여주고 최종적인 map의 사이즈를 줄여주게 된다.

또한 각 layer에서 값의 변동이 큰 것을 방지하기 위하여 Max filter를 사용하는 경우도 있다. 이 것은 전에 그냥 꽃의 유무를 판별하는 네트워크에서 맨 마지막단에 Max를 넣어 그 결과가 1에 가까웠다면 꽃이 존재한다는 것에서 유래하였다. 이것을 각 layer에 가져온 것이다. 그래서 각각의 region에 가장 큰 값을 가져와 다음단에 넘긴다. 이것을 max pooling이라고 한다.




사실 max pooling만 사용하면 그냥 이미지 한번 scan한것을 다시 한번 더 scan하는 것 밖에 안된다. 그래서 더 효율적으로 사용하기 위하여 stride도 같이 사용한다.




이렇게 사용하면 map전체의 크기를 줄일 수 있고 이것을 down sampling이라고 한다.
Max pool을 사용한 전체적인 네트워크는 아래와 같다.

또한 각각의 scan한 것을 여러번 겹쳐서 할 수 있다. 즉 여러개의 filter를 사용할 수 있는 것이다.
그리고 지금까지 했던 모든 structure를 Convolutional Neural Network 즉 CNN이라고 한다.

1-D convolution
위에서는 2-D convolution을 다루었는데 이번에는 1-D convolutoin을 다뤄본다. 기본적인 틀은 다를 것이 없다. 하지만 이미지는 정적이였다면 1-D는 시간에 따라 움직이게 된다. 예를들어 목소리의 파형 체크 같은 것이다.

그 과정은 아래와 같다. 각각의 시간의 구간을 나누어서 진행한다.







위의 과정을 Time-Delay Neural Network라고 한다.